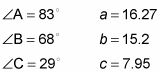¿Cómo resolver un triángulo cuando se conoce dos medidas de los ángulos
Si conoces a dos medidas de los ángulos y una longitud de lado de un triángulo, puede utilizar la
Ley de los senos para encontrar las partes que faltan de triángulo. En este caso, lo que necesita saber bien dos ángulos y el lado entre ellos (de ángulo del lado del ángulo, o ASA), o dos ángulos y un lado consecutiva (del lado del ángulo-ángulo o AAS).Cada vez que te dan dos ángulos, se puede encontrar el tercero inmediatamente y trabajar desde allí. En ambos casos, usted puede encontrar exactamente una solución para el triángulo en cuestión.
Resolver un triángulo con ASA
Un triángulo ASA significa que te dan dos ángulos y el lado entre ellos en un problema. Por ejemplo, un problema podría afirmar que
como se muestra en la figura. También puede que le den
Esta figura tiene todas las piezas dadas y desconocidos etiquetados para usted.
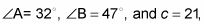
Para encontrar la información que falta a la Ley de los senos, siga estos pasos:
Determinar la medida del tercer ángulo.
Como regla,
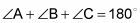
Así enchufando lo que sabe sobre los ángulos de este problema, puede resolver para el ángulo faltante:
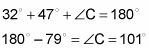
Establecer la fórmula Ley de los senos, completando lo que sabes.
Teniendo en cuenta que la fórmula de la Ley de los senos se ve así:
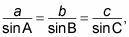
la fórmula aquí configura así:
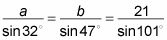
Definir una fracción con un numerador desconocida y la fracción con un numerador conocido iguales entre sí y cruzar multiplican.
Si utiliza, dicen, la primera y tercera fracciones, la ecuación parece a esto:
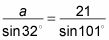
Multiplicador de la Cruz, que tiene
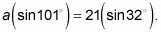
Encuentra la aproximación decimal del lado que falta usando la calculadora.
Porque el pecado 101 grados es sólo un número, se puede dividir ambos lados de la ecuación por ella para aislar la variable:
Repita los pasos 3 y 4 para resolver para el otro lado que falta.
Ajuste de la segunda y tercera fracciones iguales entre sí, usted tiene esta ecuación:
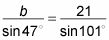
Esta ecuación se convierte en
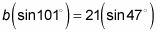
cuando cruzas multiplican. Aislar la variable y resolver para ello:
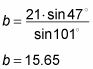
Indique todas las partes del triángulo como su respuesta final.
Algunas respuestas pueden ser aproximada, así que asegúrese de mantener los signos adecuados:
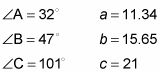
Resolver un triángulo con AAS
En muchos problemas trigonométricas, te dan dos ángulos y un lado que no está entre ellos. Este tipo de problema se llama un problema de AAS. Por ejemplo, se le puede dar
como se muestra en esta figura.
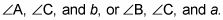
Tenga en cuenta que si usted comienza a lado b y se mueven hacia la izquierda alrededor del triángulo, se llega a
Esta comprobación es una buena manera de comprobar si un triángulo es un ejemplo de AAS.
Después de encontrar el tercer ángulo, un problema de AAS sólo se convierte en un caso especial de ASA. Estos son los pasos para resolver:
Determinar la medida del tercer ángulo.
Puedes decir eso
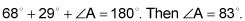
Establecer la fórmula Ley de los senos, completando lo que sabes.
Definir una fracción con un numerador desconocida y la fracción con un numerador conocido iguales entre sí y luego cruzar multiplican.
Digamos que usted elige utilizar la y b:
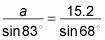
Multiplicador de la Cruz, que tiene
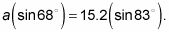
Resuelva para la parte que falta.
Usted divide por el pecado 68 grados, por lo que
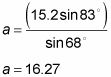
Repita los pasos 3 y 4 para resolver para el otro lado que falta.
Ajuste b y c iguales entre sí, usted tiene esta ecuación:
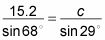
Multiplican Cruz:
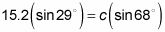
Divida por el pecado 68 grados para aislar la variable y resolver:
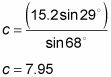
Indique todas las partes del triángulo como su respuesta final.
Su respuesta final establece de la siguiente manera:
-
Matemáticas normas fundamentales comunes: similitud, triángulos rectángulos, y trigonometría -
La aplicación de las fórmulas de suma y diferencia de los cosenos para encontrar el coseno de la suma o diferencia de dos ángulos -
Cómo calcular un ángulo utilizando funciones trigonométricas inversas -
¿Cómo resolver un triángulo cuando se sabe de dos longitudes de los lados consecutivos (ssa) -
La clasificación de tres tipos de triángulos -
Problemas de la práctica de la geometría con triángulos y polígonos
Familiarización con ángulos Los ángulos son uno de los elementos básicos de los triángulos y otros polígonos de construcción. Hay cinco tipos de ángulos: agudo, recto, obtuso, recto, y el reflejo. Usted ve ángulos en casi todas las páginas de cualquier libro de…
Cómo calcular el área de un polígono regular LA polígono regular es equilátero (tiene lados iguales) y equiangular (tiene ángulos iguales). Para encontrar el área de un polígono regular, se utiliza un apotema - un segmento que une el centro del polígono al punto medio de cualquier lado y…
Cómo utilizar el teorema del ángulo bisectriz El teorema de ángulo-Bisectriz establece que si un rayo biseca un ángulo de un triángulo, a continuación, se divide el lado opuesto en segmentos que son proporcionales a los otros dos lados. La siguiente figura ilustra esto.El teorema de ángulo…
Identificar escaleno, isósceles y triángulos equiláteros Los triángulos se clasifican según la longitud de sus lados o la medida de sus ángulos. Estas clasificaciones vienen de tres en tres, al igual que los lados y ángulos de sí mismos.Las siguientes son las clasificaciones de triángulos basada en…
La identificación de triángulos por sus ángulos Se puede clasificar triángulos por sus ángulos, así como por sus lados. Las clasificaciones basadas en ángulos son como sigue:Triángulo aguda: Un triángulo con tres ángulos agudos (menos de 90 # 176-).Triángulo obtuso: Un triángulo con un…
Triángulos trigonométricas básicas Todo por su cuenta, los ángulos son sin duda muy emocionante. Pero los puso en un triángulo, y usted tiene la guinda del pastel. Triángulos son una de las figuras geométricas estudiadas con más frecuencia. Los ángulos que forman el triángulo…
Encuentre el área de un triángulo con asa Cuando se tienen dos ángulos en un triángulo y el lado entre ellos (ASA), puede utilizar trigonométrica para hallar el área del triángulo. Las fórmulas van como sigue.En el triángulo Abecedario, si las medidas de los lados son la, b, y c…
Cómo determinar la altura de un árbol ¿Qué función trigonométrica se debe utilizar para determinar la altura de un árbol? Supongamos que usted está volando una cometa, y se ve atrapado en la parte superior de un árbol. Has dejado a cabo los 100 pies de cadena para el kite, y el…
¿Cómo resolver una ecuación de trigonometría utilizando la fórmula cuadrática Cuando el factor trigonometría ecuaciones de segundo grado, la vida es buena. Cuando no lo hacen, usted todavía puede sobrevivir, gracias a que la fórmula cuadrática maravilloso. En caso de que hayas olvidado la fórmula exacta, aquí está.La…
Cómo utilizar la ley de los senos con un triángulo Cuando usted ya conoce dos ángulos en un triángulo, así como uno de los lados, como en el caso de AAS o AAS, se puede utilizar el ley de los senos para encontrar las medidas de los otros dos lados. Esta ley utiliza las proporciones de los lados…
Cómo usar la trigonometría para encontrar el área de un triángulo A veces, la búsqueda de una medida que no es tan fácil. Puede que tenga que hacer frente a una forma irregular, como un triángulo, o incluso calcular su camino alrededor de un objeto fijo. En cualquier caso, puede utilizar la trigonometría para…
La función coseno: adyacente sobre la hipotenusa La función trigonométrica coseno, abreviado cos, funciona mediante la formación de esta relación: adyacente / hipotenusa. En la figura, se ve que los cosenos de los dos ángulos son los siguientes:La situación con las proporciones es el mismo…