Cómo utilizar el teorema del ángulo bisectriz
El teorema de ángulo-Bisectriz establece que si un rayo biseca un ángulo de un triángulo, a continuación, se divide el lado opuesto en segmentos que son proporcionales a los otros dos lados. La siguiente figura ilustra esto.
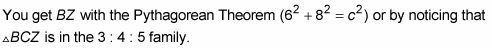
El teorema de ángulo bisectriz implica una proporción - al igual que con triángulos semejantes. Pero tenga en cuenta que nunca obtener triángulos semejantes cuando bisecta un ángulo de un triángulo (a menos que bisecta vértice de un triángulo isósceles, en cuyo caso la bisectriz divide el triángulo en dos triángulos congruentes).
No olvide el ángulo-Bisectriz teorema. (Por alguna razón, los estudiantes a menudo se olvidan de este teorema.) Así que cada vez que vea un triángulo con uno de sus ángulos atravesada, considere el uso del teorema.
¿Qué tal un problema de ángulo bisectriz? ¿Por qué? Oh, sólo Bcuz.
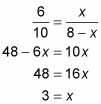
Teniendo en cuenta: Diagrama como se muestra
Encontrar: 1.) BZ, CU, UZ, y BU y 2.) El área del triángulo BCU y el triángulo BUZ
Encontrar BZ, CU, UZ, y BU.
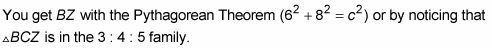
Es un triángulo 6-8-10, por lo BZ es 10.
A continuación, establezca CU igual a X. UZ a continuación, se convierte en 8 - X. Establecer la proporción de ángulo bisectriz y resuelve para X:
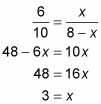
Así CU es 3 y UZ es 5.
El Teorema de Pitágoras y luego le da BU:
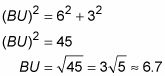
Calcular el área del triángulo BCU y el triángulo BUZ.
Ambos triángulos tienen una altura de 6 (cuando se utiliza el segmento CU y el segmento de UZ como sus bases), por lo que sólo tiene que utilizar la fórmula del área del triángulo:
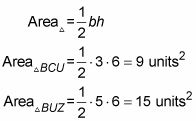
Tenga en cuenta que la relación de las áreas de estos triángulos, 9: 15 (que se reduce a 3: 5), es igual a la relación de las bases de los triángulos ', 3: 5. Esta igualdad lleva a cabo cada vez que un triángulo está dividido en dos triángulos con un segmento de uno de sus vértices para el lado opuesto (si o no este segmento corta el ángulo del vértice exactamente por la mitad).
Descubriendo ternas pitagóricas El teorema de Pitágoras es sin duda uno de los teoremas más famosos de toda la matemática. Matemáticos y laicos por igual han estudiado durante siglos, y la gente ha demostrado de muchas maneras diferentes. (Incluso el presidente James Garfield…
Encontrar la altitud de un triángulo La altitud de un triángulo es un segmento de un vértice del triángulo hacia el lado opuesto (o a la extensión del lado opuesto si es necesario) que es perpendicular a la opuesta lateral del lado opuesto se llama la base. (Se utiliza la…
Geometría fórmulas y reglas para triángulos Las pirámides de tres ángulos, bidimensionales conocidos como triángulos son uno de los componentes básicos de la geometría (sin embargo de tres picos que sean). Triángulos, por supuesto, tienen sus propias fórmulas para encontrar el área y…
Problemas de la práctica de la geometría con triángulos y polígonos LA polígono es una figura geométrica que tiene al menos tres lados. El triángulo es el polígono más básico. Usted encontrará las siguientes fórmulas y propiedades útiles al responder a las preguntas que implican desigualdades triángulo,…
Cómo calcular el área de un cometa Usted calcula el área de un cometa mediante el uso de las longitudes de sus diagonales. He aquí un ejemplo: ¿cuál es el área de la cometa COMETA en la siguiente figura?Para los problemas de la cometa zona (y algunas veces otros problemas…
Cómo calcular el área de un paralelogramo, cometa, o trapezoidal Las fórmulas del área para el paralelogramo, cometa, y trapezoide se basan en el área de un rectángulo. Las siguientes figuras muestran cómo cada uno de estos tres cuadriláteros se refiere a un rectángulo, y la siguiente lista te da los…
¿Cómo encontrar el incentro, circuncentro y ortocentro de un triángulo Cada triángulo tiene tres "centros" - un incentro, el circuncentro, ortocentro y un - que se encuentran en la intersección de los rayos, líneas y segmentos asociados con el triángulo:Centrado: Cuando tres bisectrices de un triángulo se…
¿Cómo demostrar triángulos semejantes con sas ~ Usted puede probar que los triángulos son similares utilizando el método SAS ~ (Side-Angle-Side). SAS ~ establece que si dos lados de un triángulo son proporcionales a dos lados de otro triángulo y los ángulos incluidos son congruentes,…
¿Cómo demostrar triángulos semejantes usando el teorema de aa Usted puede utilizar el método de AA (ángulo-ángulo) para demostrar que los triángulos son semejantes. El teorema de AA establece que si dos ángulos de un triángulo son congruentes con dos ángulos de otro triángulo, entonces los triángulos…
¿Cómo demostrar triángulos semejantes con sss ~ Usted puede probar que los triángulos son similares utilizando el método SSS ~ (Side-Side-Side). SSS ~ establece que si las relaciones de los tres pares de lados de dos triángulos correspondientes son iguales, entonces los triángulos son…
Cómo resolver problemas de triángulos similares con el teorema de lado divisor Usted puede resolver ciertos problemas de triángulos similares utilizando el Side-divisor teorema. Este teorema afirma que si una línea es paralela a un lado de un triángulo y que interseca los otros dos lados, se divide esos lados…
Identificar escaleno, isósceles y triángulos equiláteros Los triángulos se clasifican según la longitud de sus lados o la medida de sus ángulos. Estas clasificaciones vienen de tres en tres, al igual que los lados y ángulos de sí mismos.Las siguientes son las clasificaciones de triángulos basada en…