¿Cómo encontrar el incentro, circuncentro y ortocentro de un triángulo

Cada triángulo tiene tres "centros" - un incentro, el circuncentro, ortocentro y un - que se encuentran en la intersección de los rayos, líneas y segmentos asociados con el triángulo:

• Centrado: Cuando tres bisectrices de un triángulo se intersecan (un bisectriz es un rayo que corta en un ángulo medio) - el incentro es el centro de un círculo inscrita en (dibujado en el interior) el triángulo.

• Circumcenter: Cuando las tres mediatrices de los lados de un triángulo se intersecan (una mediatriz es una línea que forma un ángulo de 90 ° con un segmento y corta el segmento en el medio) - el circuncentro es el centro de un círculo circunscrito sobre (dibujado alrededor) el triángulo.

• Ortocentro: Cuando tres alturas del triángulo se intersecan. La altitud de un triángulo es un segmento de un vértice del triángulo hacia el lado opuesto (o a la extensión del lado opuesto si es necesario) que es perpendicular a la opuesta lateral del lado opuesto se llama el base.

Encontrar el incentro

Usted encuentra incentro de un triángulo en la intersección de tres bisectrices del triángulo. Esta ubicación le da el incentro una propiedad interesante: El incentro es igualmente lejos de los tres lados del triángulo. Ningún otro punto tiene esta calidad. Incentros, como centroides, siempre dentro de sus triángulos.

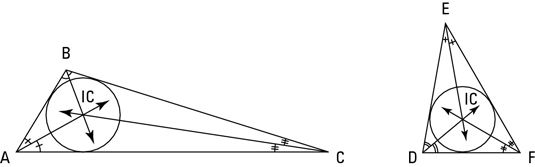
La figura de arriba muestra dos triángulos con sus incentros y círculos inscritos, o En circulos (círculos dibujados dentro de los triángulos de manera que los círculos apenas tocan los lados de cada triángulo). Los incentros son los centros de los incircles. (No hablar de esto "en" cosas demasiado si quieres estar en el in-multitud.)

Encontrar el circuncentro

Usted encuentra un triángulo de circuncentro en la intersección de las mediatrices de los lados del triángulo. Esta ubicación le da el circuncentro una propiedad interesante: el circuncentro es igualmente lejos de los tres vértices del triángulo.

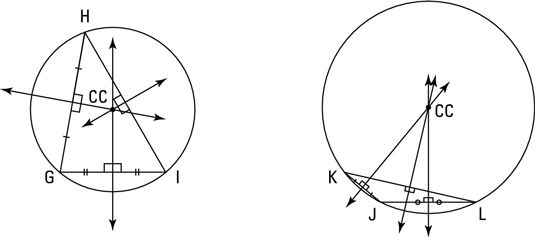
La figura de arriba muestra dos triángulos con sus circuncentros y círculos circunscritos, o circunferencias circunscritas (círculos dibujados alrededor de los triángulos de manera que los círculos pasan por los vértices de cada triángulo). Los circuncentros son los centros de las circunferencias circunscritas.

Se puede ver en la figura anterior que, a diferencia de centroides y incentros, un circuncentro es a veces fuera del triángulo. El circuncentro es

• Dentro de todos los triángulos agudos

• Fuera de todos los triángulos obtusos

• En todos los triángulos rectángulos (en el punto medio de la hipotenusa)

Encontrar el ortocentro

Echa un vistazo a la siguiente figura para ver un par de orthocenters. Usted encuentra ortocentro de un triángulo en la intersección de sus alturas. A diferencia del centro de gravedad, incentro y circuncentro - todos los cuales se encuentra en un punto interesante del triángulo (centro del triángulo de la gravedad, el punto equidistante de los lados del triángulo, y el punto equidistante de los vértices del triángulo, respectivamente), un triángulo de ortocentro no radica en un punto con tales características agradables. Bueno, tres de cada cuatro no está mal.

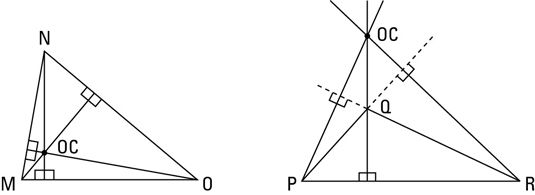
Pero conseguir una carga de esto: Mire de nuevo a los triángulos en la figura. Tome los cuatro puntos marcados de uno u otro triángulo (los tres vértices más el ortocentro). Si comete un triángulo de tres de esos cuatro puntos, el cuarto punto es el ortocentro de ese triángulo. Muy dulce, ¿eh?

Orthocenters siguen la misma regla que circuncentros (tenga en cuenta que ambos orthocenters y circuncentros implican líneas perpendiculares - altitudes y mediatrices): El ortocentro es

• Dentro de todos los triángulos agudos

• Fuera de todos los triángulos obtusos

• En todos los triángulos rectángulos (en el vértice en ángulo recto)