La identificación de la 30 - triángulo de 90 grados - 60
El 30 - 60 - 90 grado triángulo está en la forma de un medio de un triángulo equilátero, de corte recto por la mitad a lo largo de su altitud. Tiene ángulos de 30 # 176-, 176- # 60, # 90 y 176- y los lados en la proporción de
La siguiente figura muestra un ejemplo.
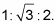
Conozca este triángulo haciendo un par de problemas. Encuentra las longitudes de los lados desconocidos en triángulo UMP y el triángulo IRE en la siguiente figura.
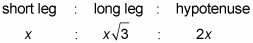
Usted puede resolver 30 # 176-- 60 # 176-- 90 # 176- triángulos con el método manual o el método de la calle inteligente.
Utilizando el método de libros de texto
El método de libros de texto comienza con la relación de los lados de la primera figura:
En el triángulo UMP, la hipotenusa es 10, por lo que el grupo 2X igual a 10 y resolver para X, consiguiendo X = 5. Ahora sólo tiene que enchufar 5 en la X's, y usted tiene el triángulo UMP:
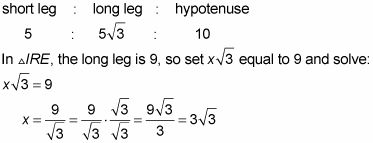
Enchufe el valor de X, y ya está:
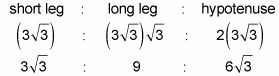
Utilizando el método de la calle inteligente
Aquí está el método de la calle inteligente para el 30 # 176-- 60 # 176-- 90 # 176- triángulo.
El uso de este hecho, haga lo siguiente:
La relación entre la pata corta y la hipotenusa es una obviedad: la hipotenusa es dos veces más que la pata corta. Así que si usted sabe que uno de ellos, puede obtener el otro en la cabeza.
Si conoce la pierna corta y desea calcular la pata larga (un más tiempo cosa), que multiplicar por la raíz cuadrada de 3. Si conoce la pierna larga y desea calcular la longitud de la pierna corta (un más corto cosa), que dividir por la raíz cuadrada de 3.
Pruebe el método de la calle inteligente con los triángulos en la segunda figura. La hipotenusa del triángulo en UMP es 10, por lo que primero se corta por la mitad para obtener la longitud de la pierna corta, que es por lo tanto 5.
Las 30 # 176-- 60 # 176-- 90 # 176- triángulos casi siempre tienen una o dos lados cuyas longitudes contener una raíz cuadrada. En cualquier caso, el largo de la pierna es el impar hacia fuera. Las tres partes podrían contener raíces cuadradas, pero es imposible que ninguno de los bandos - que conduce a la siguiente advertencia.
Debido a que al menos un lado de un 30 # 176-- 60 # 176-- 90 # 176- triángulo debe contener una raíz cuadrada, un 30 # 176-- 60 # 176-- 90 # 176- triángulo no puede pertenecer a cualquiera de las familias triángulo triples pitagóricos. Así que no cometa el error de pensar que un 30 # 176-- 60 # 176-- 90 # 176- triángulo es, digamos, en el 8: 15: 17 de la familia o que cualquier triángulo que está en uno de la triple pitagórico familias triángulo es también un 30 # 176-- 60 # 176-- 90 # 176- triángulo. No hay coincidencia entre el 30 # 176-- 60 # 176-- 90 # 176- triángulo y cualquiera de los triángulos triples pitagóricos y sus familias.
Determinar el área de un triángulo desde su base y la altura Si conoce la base y la altura de un triángulo, puede utilizar una fórmula probada y verdadera para encontrar su área. Es probable que primero encontró con la fórmula básica área del triángulo en aproximadamente sexto o séptimo grado. Si ha…
La determinación de la superficie de un triángulo equilátero Para calcular el área de un triángulo - para la mayoría de tipos de triángulos - lo que necesita saber de base y la altura del triángulo. Sin embargo, con un triángulo equilátero, todo lo que necesitas saber es la longitud de uno de sus…
Descubriendo ternas pitagóricas El teorema de Pitágoras es sin duda uno de los teoremas más famosos de toda la matemática. Matemáticos y laicos por igual han estudiado durante siglos, y la gente ha demostrado de muchas maneras diferentes. (Incluso el presidente James Garfield…
Encontrar la altitud de un triángulo La altitud de un triángulo es un segmento de un vértice del triángulo hacia el lado opuesto (o a la extensión del lado opuesto si es necesario) que es perpendicular a la opuesta lateral del lado opuesto se llama la base. (Se utiliza la…
Geometría fórmulas y reglas para triángulos Las pirámides de tres ángulos, bidimensionales conocidos como triángulos son uno de los componentes básicos de la geometría (sin embargo de tres picos que sean). Triángulos, por supuesto, tienen sus propias fórmulas para encontrar el área y…
Problemas de la práctica de la geometría con triángulos y polígonos LA polígono es una figura geométrica que tiene al menos tres lados. El triángulo es el polígono más básico. Usted encontrará las siguientes fórmulas y propiedades útiles al responder a las preguntas que implican desigualdades triángulo,…
Cómo calcular el área de un polígono regular LA polígono regular es equilátero (tiene lados iguales) y equiangular (tiene ángulos iguales). Para encontrar el área de un polígono regular, se utiliza un apotema - un segmento que une el centro del polígono al punto medio de cualquier lado y…
¿Cómo encontrar el incentro, circuncentro y ortocentro de un triángulo Cada triángulo tiene tres "centros" - un incentro, el circuncentro, ortocentro y un - que se encuentran en la intersección de los rayos, líneas y segmentos asociados con el triángulo:Centrado: Cuando tres bisectrices de un triángulo se…
Identificar escaleno, isósceles y triángulos equiláteros Los triángulos se clasifican según la longitud de sus lados o la medida de sus ángulos. Estas clasificaciones vienen de tres en tres, al igual que los lados y ángulos de sí mismos.Las siguientes son las clasificaciones de triángulos basada en…
La identificación de la 45 - triángulo de 90 grados - 45 Un 45 a 45 - 90 grados triángulo (o triángulo rectángulo isósceles) es un triángulo con ángulos de 45 # 176-, 176- 45 # y 90 # 176- y los lados de la relación entreTenga en cuenta que se trata de la forma de la mitad de un cuadrado, corte a…
La identificación de triángulos por sus ángulos Se puede clasificar triángulos por sus ángulos, así como por sus lados. Las clasificaciones basadas en ángulos son como sigue:Triángulo aguda: Un triángulo con tres ángulos agudos (menos de 90 # 176-).Triángulo obtuso: Un triángulo con un…
Trabajando con triángulos triples pitagóricos Los primeros cuatro triángulos triples pitagóricos son los favoritos de la geometría de problemas de decisión. Estas triples - especialmente el primero y el segundo en la lista que sigue - pop-up por todo el lugar en los libros de geometría.…