Trabajando con triángulos triples pitagóricos
Los primeros cuatro triángulos triples pitagóricos son los favoritos de la geometría de problemas de decisión. Estas triples - especialmente el primero y el segundo en la lista que sigue - pop-up por todo el lugar en los libros de geometría. (Nota: Los dos primeros números en cada uno de los triángulos triples son las longitudes de las piernas, y el tercero, el número más grande es la longitud de la hipotenusa).
Conteúdo
Estos son los primeros cuatro triángulos triples pitagóricos:
El triángulo 3-4-5
El 05/12/13 triángulo
El 07/24/25 triángulo
El 08/15/17 triángulo
Harías bien que memorizar estos Fab Four para que pueda reconocer rápidamente en los exámenes.
La formación de triángulos triples pitagóricos irreductibles
Como alternativa a contar ovejas alguna noche, es posible que desee para ver cuántos triángulos triples pitagóricos puede ocurrir.
Los tres primeros en la lista anterior siguen un patrón. Considere el 05/12/13 triángulo, por ejemplo. La plaza de los más pequeños, la pierna extraño
es la suma de la pierna más larga y la hipotenusa (12 + 13 = 25). Y la pierna más larga y la hipotenusa son siempre números consecutivos. Este patrón hace que sea fácil de generar la mayor cantidad de más triángulos que quieras. Esto es lo que hace:
Tome cualquier número impar y la Plaza de la misma.
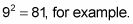
Encuentra los dos números consecutivos que suman a este valor.
40 + 41 = 81
A menudo sólo puede llegar a los dos números de la parte superior de su cabeza, pero si no se ve de inmediato, simplemente restar 1 a partir del resultado en el paso 1 y luego dividir el resultado por 2:
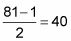
Ese resultado y el siguiente número más grande son sus dos números.
Escribe el número que al cuadrado y los dos números de la Etapa 2 en orden consecutivo el nombre de su triple.
Ahora tiene otra Pitágoras triángulo triples: 9-40-41.
Estos son los próximos triángulos triples pitagóricos que siguen este patrón:
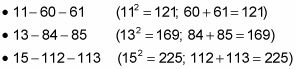
Esta lista es interminable - capaz de lidiar con el peor caso posible de insomnio. Y en cuenta que cada triángulo en esta lista es irreducible- es decir, no es un múltiplo de algunos de triple triángulo de Pitágoras más pequeño (en contraste con el 6-8-10 triángulo, por ejemplo, que no es irreducible porque es la 3-4- 5 triángulo doble).
Cuando usted hace un nuevo triángulo de triple pitagórico (como el 06/08/10) por la voladura de una más pequeña (el 3-4-5), se obtiene triángulos con la misma forma exacta. Pero cada irreducible Pitágoras triángulo de triple tiene una forma diferente de todos los otros triángulos irreductibles.
La formación de nuevos triángulos triples pitagóricos
El 08/15/17 triángulo es el primero de Pitágoras triángulo de triple que no sigue el patrón mencionado anteriormente. He aquí cómo usted genera triples que siguen el patrón de 08.15.17:
Tome cualquier múltiplo de 4.
Digamos que usted elija 12.
Media plaza de la misma.
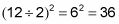
Tome el número de la Etapa 1 y los dos números impares a cada lado de el resultado en el paso 2 para obtener un triángulo de Pitágoras triple.
12-35-37
Los próximos triples en este conjunto infinito son
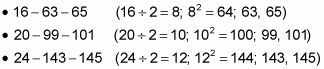
Por cierto, puede utilizar este proceso para el resto de los números pares (los que no son múltiplos de 4), tales como 10, 14, 18, y así sucesivamente. Pero se obtiene un triángulo como el 10/24/26 triángulo, que es el 05/12/13 Pitágoras triángulo triple de soplado hasta el doble de su tamaño, en lugar de un triángulo irreductible, en forma de forma exclusiva.
La clasificación de tres tipos de triángulos Los triángulos se clasifican según la longitud de sus lados o la medida de sus ángulos. Estas clasificaciones vienen de tres en tres, al igual que los lados y ángulos de sí mismos. Es decir, un triángulo tiene tres lados, y tres términos…
La determinación de la superficie de un triángulo equilátero Para calcular el área de un triángulo - para la mayoría de tipos de triángulos - lo que necesita saber de base y la altura del triángulo. Sin embargo, con un triángulo equilátero, todo lo que necesitas saber es la longitud de uno de sus…
Descubriendo ternas pitagóricas El teorema de Pitágoras es sin duda uno de los teoremas más famosos de toda la matemática. Matemáticos y laicos por igual han estudiado durante siglos, y la gente ha demostrado de muchas maneras diferentes. (Incluso el presidente James Garfield…
Geometría fórmulas y reglas para triángulos Las pirámides de tres ángulos, bidimensionales conocidos como triángulos son uno de los componentes básicos de la geometría (sin embargo de tres picos que sean). Triángulos, por supuesto, tienen sus propias fórmulas para encontrar el área y…
Problemas de la práctica de la geometría con triángulos y polígonos LA polígono es una figura geométrica que tiene al menos tres lados. El triángulo es el polígono más básico. Usted encontrará las siguientes fórmulas y propiedades útiles al responder a las preguntas que implican desigualdades triángulo,…
Cómo calcular el área de un hexágono regular Una forma de encontrar el área de un hexágono regular es de primera división en triángulos equiláteros. También es necesario utilizar un apotema - un segmento que une el centro de un polígono regular hasta el punto medio de cualquier lado y…
¿Cómo encontrar el incentro, circuncentro y ortocentro de un triángulo Cada triángulo tiene tres "centros" - un incentro, el circuncentro, ortocentro y un - que se encuentran en la intersección de los rayos, líneas y segmentos asociados con el triángulo:Centrado: Cuando tres bisectrices de un triángulo se…
Cómo utilizar el teorema del ángulo bisectriz El teorema de ángulo-Bisectriz establece que si un rayo biseca un ángulo de un triángulo, a continuación, se divide el lado opuesto en segmentos que son proporcionales a los otros dos lados. La siguiente figura ilustra esto.El teorema de ángulo…
Identificar escaleno, isósceles y triángulos equiláteros Los triángulos se clasifican según la longitud de sus lados o la medida de sus ángulos. Estas clasificaciones vienen de tres en tres, al igual que los lados y ángulos de sí mismos.Las siguientes son las clasificaciones de triángulos basada en…
La identificación de la 45 - triángulo de 90 grados - 45 Un 45 a 45 - 90 grados triángulo (o triángulo rectángulo isósceles) es un triángulo con ángulos de 45 # 176-, 176- 45 # y 90 # 176- y los lados de la relación entreTenga en cuenta que se trata de la forma de la mitad de un cuadrado, corte a…
La identificación de la 30 - triángulo de 90 grados - 60 El 30 - 60 - 90 grado triángulo está en la forma de un medio de un triángulo equilátero, de corte recto por la mitad a lo largo de su altitud. Tiene ángulos de 30 # 176-, 176- # 60, # 90 y 176- y los lados en la proporción deLa siguiente…
La identificación de triángulos por sus ángulos Se puede clasificar triángulos por sus ángulos, así como por sus lados. Las clasificaciones basadas en ángulos son como sigue:Triángulo aguda: Un triángulo con tres ángulos agudos (menos de 90 # 176-).Triángulo obtuso: Un triángulo con un…