Cómo resolver problemas de triángulos similares con el teorema de lado divisor
Usted puede resolver ciertos problemas de triángulos similares utilizando el Side-divisor teorema. Este teorema afirma que si una línea es paralela a un lado de un triángulo y que interseca los otros dos lados, se divide esos lados proporcionalmente. Vea la siguiente figura.
Echa un vistazo a el siguiente problema, que muestra este teorema en acción:
Aquí está la prueba:
Entonces, debido a que ambos triángulos contienen ángulo S, los triángulos son semejantes por AA (ángulo-ángulo).
Ahora busca X y y.
Y aquí está la solución para y: En primer lugar, no caer en la trampa y la conclusión de que y = 4. Side y parece que debería ser igual a 4 por dos razones: En primer lugar, se podría llegar a la conclusión errónea de que el triángulo TRS es un triángulo rectángulo 3-4-5. Pero nada de lo que dice ese triángulo TRS es un ángulo recto, por lo que no se puede concluir que.
En segundo lugar, cuando ves las relaciones de 9: 3 (junto segmento QS) Y 15: 5 (lo largo del segmento PS, después de resolver por X), Ambos de los cuales se reducen a 3: 1, parece PQ y y debe estar en la misma proporción de 3: 1. Eso haría que PQ : y 12: 4 ratio, que a su vez conduce a la respuesta equivocada que y es 4. La respuesta sale mal porque este proceso de pensamiento equivale a utilizar el Lado-divisor Teorema de los lados que no están divididos - que no se les permite hacer.
No utilice el lateral divisor teorema de lados que no se dividen. Puede utilizar el teorema-Side divisor solamente para los cuatro segmentos en los lados de división del triángulo. No lo utilice para los lados paralelos, que están en una relación diferente. Por los lados paralelos, utilice proporciones similares-triángulo. (Siempre que un triángulo está dividido por una línea paralela a uno de sus lados, el triángulo creado es similar a la, gran triángulo original).
Así que finalmente, la forma correcta de llegar y es utilizar una proporción similar triángulo ordinaria. Los triángulos en este problema se colocan de la misma manera, por lo que puede escribir lo siguiente:
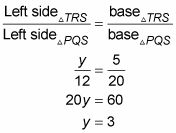
Eso es un envoltorio.
-
Matemáticas normas fundamentales comunes: similitud, triángulos rectángulos, y trigonometría -
¿Cómo medir los triángulos -
¿Cómo trabajar con triángulos 30-60-90 grados -
Aplicando el teorema de Pitágoras -
La clasificación de tres tipos de triángulos -
La determinación de la superficie de un triángulo equilátero
Descubriendo ternas pitagóricas El teorema de Pitágoras es sin duda uno de los teoremas más famosos de toda la matemática. Matemáticos y laicos por igual han estudiado durante siglos, y la gente ha demostrado de muchas maneras diferentes. (Incluso el presidente James Garfield…
Geometría fórmulas y reglas para triángulos Las pirámides de tres ángulos, bidimensionales conocidos como triángulos son uno de los componentes básicos de la geometría (sin embargo de tres picos que sean). Triángulos, por supuesto, tienen sus propias fórmulas para encontrar el área y…
Problemas de la práctica de la geometría con triángulos y polígonos LA polígono es una figura geométrica que tiene al menos tres lados. El triángulo es el polígono más básico. Usted encontrará las siguientes fórmulas y propiedades útiles al responder a las preguntas que implican desigualdades triángulo,…
¿Cómo encontrar el incentro, circuncentro y ortocentro de un triángulo Cada triángulo tiene tres "centros" - un incentro, el circuncentro, ortocentro y un - que se encuentran en la intersección de los rayos, líneas y segmentos asociados con el triángulo:Centrado: Cuando tres bisectrices de un triángulo se…
¿Cómo demostrar triángulos semejantes con sas ~ Usted puede probar que los triángulos son similares utilizando el método SAS ~ (Side-Angle-Side). SAS ~ establece que si dos lados de un triángulo son proporcionales a dos lados de otro triángulo y los ángulos incluidos son congruentes,…
¿Cómo demostrar triángulos semejantes usando el teorema de aa Usted puede utilizar el método de AA (ángulo-ángulo) para demostrar que los triángulos son semejantes. El teorema de AA establece que si dos ángulos de un triángulo son congruentes con dos ángulos de otro triángulo, entonces los triángulos…
¿Cómo demostrar triángulos semejantes con sss ~ Usted puede probar que los triángulos son similares utilizando el método SSS ~ (Side-Side-Side). SSS ~ establece que si las relaciones de los tres pares de lados de dos triángulos correspondientes son iguales, entonces los triángulos son…
¿Cómo resolver un problema-tangente común los problema-tangente común se nombra para el segmento única tangente que es tangente a dos círculos. Su objetivo es encontrar la longitud de la tangente. Estos problemas son un poco complicado, pero deben hacer que poca dificultad si se utiliza…
¿Cómo resolver problemas con el teorema de altitud-0n-hipotenusa En un triángulo rectángulo, la altitud que es perpendicular a la hipotenusa tiene una propiedad especial: crea dos triángulos más pequeños de derecha que son a la vez similar al triángulo original derecha.Altitud-on-Hipotenusa Teorema: Si una…
Cómo utilizar el teorema del ángulo bisectriz El teorema de ángulo-Bisectriz establece que si un rayo biseca un ángulo de un triángulo, a continuación, se divide el lado opuesto en segmentos que son proporcionales a los otros dos lados. La siguiente figura ilustra esto.El teorema de ángulo…
Identificar escaleno, isósceles y triángulos equiláteros Los triángulos se clasifican según la longitud de sus lados o la medida de sus ángulos. Estas clasificaciones vienen de tres en tres, al igual que los lados y ángulos de sí mismos.Las siguientes son las clasificaciones de triángulos basada en…
La identificación de la 45 - triángulo de 90 grados - 45 Un 45 a 45 - 90 grados triángulo (o triángulo rectángulo isósceles) es un triángulo con ángulos de 45 # 176-, 176- 45 # y 90 # 176- y los lados de la relación entreTenga en cuenta que se trata de la forma de la mitad de un cuadrado, corte a…