¿Cómo resolver problemas con el teorema de altitud-0n-hipotenusa
En un triángulo rectángulo, la altitud que es perpendicular a la hipotenusa tiene una propiedad especial: crea dos triángulos más pequeños de derecha que son a la vez similar al triángulo original derecha.
Altitud-on-Hipotenusa Teorema: Si una altitud se señala a la hipotenusa de un triángulo rectángulo como se muestra en la figura anterior, a continuación,
Tenga en cuenta que las dos ecuaciones de la tercera parte del teorema son realmente sólo una idea, no dos. Funciona exactamente de la misma manera en ambos lados de la gran triángulo:
Aquí hay un problema: utilizar la figura de abajo para contestar las siguientes preguntas.
Si JL = 17 y KL = 15, ¿cuáles son JK, JM, ML, y KM?
He aquí cómo usted hace esto: JK es 8 porque tienes un triángulo 08/15/17 (o usted puede conseguir JK con el Teorema de Pitágoras). Ahora usted puede encontrar JM y ML usando la tercera parte del teorema Altitud-on-Hipotenusa:
(Los ML solución se incluye sólo para mostrar otro ejemplo del teorema, pero, obviamente, hubiera sido más fácil de conseguir ML con sólo restando JM de JL.)
Por último, utilice la segunda parte del teorema (o el teorema de Pitágoras, si lo prefiere) para obtener KM:
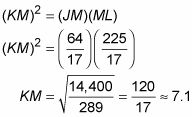
Si ML = 16 y JK = 15, ¿cuál es JM?
Set JM igual a X- a continuación, utilizar la tercera parte del teorema.
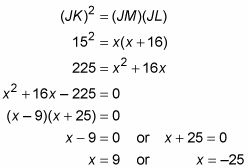
Usted sabe que una longitud no puede ser -25, por lo JM = 9. (Si tiene dificultades para ver cómo factorizar éste, usted puede usar la fórmula cuadrática para obtener los valores de X en su lugar.)
Al hacer un problema que involucra un diagrama de altitud-on-hipotenusa, no asuma que se debe utilizar la segunda o tercera parte del teorema Altitud-on-Hipotenusa. A veces, la mejor manera de resolver el problema es con el Teorema de Pitágoras. Y en otras ocasiones, puede utilizar proporciones similares-triángulo ordinarios para resolver el problema.
El siguiente problema ilustra este consejo: Utilice la siguiente figura para encontrar h, la altitud del triángulo Abecedario.
En sus marcas, listos, ya. En primer lugar obtener Corriente alterna con el Teorema de Pitágoras o por darse cuenta de que usted tiene un triángulo en el 3: 4: la familia 5 - a saber, un triángulo 09/12/15. Así Corriente alterna = 15. Entonces, a pesar de que podría terminar con el Teorema Altitud-on-Hipotenusa, pero ese enfoque es un poco complicado y podría llevar algo de trabajo. En lugar de ello, sólo tiene que utilizar una proporción similar triángulo ordinaria:
Finito.
Encontrar la altitud de un triángulo La altitud de un triángulo es un segmento de un vértice del triángulo hacia el lado opuesto (o a la extensión del lado opuesto si es necesario) que es perpendicular a la opuesta lateral del lado opuesto se llama la base. (Se utiliza la…
Geometría fórmulas y reglas para triángulos Las pirámides de tres ángulos, bidimensionales conocidos como triángulos son uno de los componentes básicos de la geometría (sin embargo de tres picos que sean). Triángulos, por supuesto, tienen sus propias fórmulas para encontrar el área y…
Problemas de la práctica de la geometría con triángulos y polígonos LA polígono es una figura geométrica que tiene al menos tres lados. El triángulo es el polígono más básico. Usted encontrará las siguientes fórmulas y propiedades útiles al responder a las preguntas que implican desigualdades triángulo,…
Fórmulas de geometría que usted debe saber A continuación se presentan algunas de las fórmulas de geometría más importantes, teoremas, propiedades, etc. que se utilizan para resolver diversos problemas. Si te quedas perplejo mientras se trabaja en un problema y no puede llegar a una…
Libro de Geometría para dummies Si estás estudiando geometría, que se está viendo en todas partes símbolos - símbolos de arcos y ángulos, líneas y triángulos, así como símbolos de las relaciones entre las líneas y ángulos y así sucesivamente. A continuación se…
Cómo calcular el área de un cometa Usted calcula el área de un cometa mediante el uso de las longitudes de sus diagonales. He aquí un ejemplo: ¿cuál es el área de la cometa COMETA en la siguiente figura?Para los problemas de la cometa zona (y algunas veces otros problemas…
¿Cómo demostrar triángulos semejantes con sss ~ Usted puede probar que los triángulos son similares utilizando el método SSS ~ (Side-Side-Side). SSS ~ establece que si las relaciones de los tres pares de lados de dos triángulos correspondientes son iguales, entonces los triángulos son…
¿Cómo resolver un problema-tangente común los problema-tangente común se nombra para el segmento única tangente que es tangente a dos círculos. Su objetivo es encontrar la longitud de la tangente. Estos problemas son un poco complicado, pero deben hacer que poca dificultad si se utiliza…
Cómo resolver problemas de triángulos similares con el teorema de lado divisor Usted puede resolver ciertos problemas de triángulos similares utilizando el Side-divisor teorema. Este teorema afirma que si una línea es paralela a un lado de un triángulo y que interseca los otros dos lados, se divide esos lados…
Cómo utilizar el teorema del ángulo bisectriz El teorema de ángulo-Bisectriz establece que si un rayo biseca un ángulo de un triángulo, a continuación, se divide el lado opuesto en segmentos que son proporcionales a los otros dos lados. La siguiente figura ilustra esto.El teorema de ángulo…
¿Cómo encontrar la distancia a través de un estanque La trigonometría es muy útil para encontrar las distancias que no se puede llegar a medir. Imagina que quieres cadena un cable diagonal a través de un estanque (para que pueda adjuntar un montón de línea de pesca y anzuelos). La distancia…
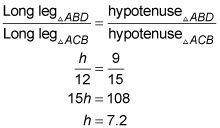
La función coseno: adyacente sobre la hipotenusa La función trigonométrica coseno, abreviado cos, funciona mediante la formación de esta relación: adyacente / hipotenusa. En la figura, se ve que los cosenos de los dos ángulos son los siguientes:La situación con las proporciones es el mismo…