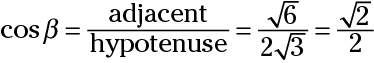La función coseno: adyacente sobre la hipotenusa
La función trigonométrica coseno, abreviado cos, funciona mediante la formación de esta relación: adyacente / hipotenusa. En la figura, se ve que los cosenos de los dos ángulos son los siguientes:
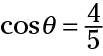
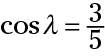
La situación con las proporciones es el mismo que con la función seno - los valores van a ser menor que o igual a 1 (este último sólo cuando el triángulo es un único segmento o cuando se trata con círculos), nunca es mayor que 1, porque la hipotenusa es el denominador.
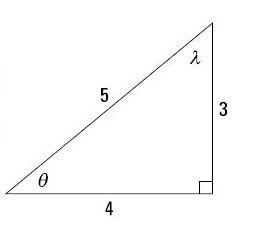
Los dos ratios para el coseno son los mismos que los de la sine - excepto los ángulos se invierten. Esta propiedad es el caso de los senos y cosenos de complementario ángulos en un triángulo rectángulo (es decir, los ángulos que se suman a 90 grados).
Si theta y lambda son los dos ángulos agudos de un triángulo rectángulo, entonces el pecado theta = lambda cos y cos theta = lambda pecado.
Ahora para un ejemplo. Para encontrar el coseno del ángulo beta en un triángulo rectángulo si las dos piernas son cada
pies de largo:
Encuentra la longitud de la hipotenusa.
Usando el teorema de Pitágoras, la2 + b2 = c2, y la sustitución de tanto la y b con la medida dada, resolver c.
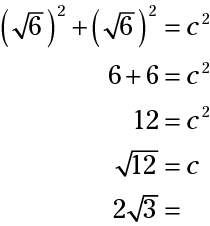
La hipotenusa es
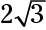
pies de largo.
Utilice la proporción de coseno, adyacente sobre la hipotenusa, para encontrar la respuesta.
-
Matemáticas normas fundamentales comunes: similitud, triángulos rectángulos, y trigonometría -
¿Cómo medir los triángulos -
La aplicación de las fórmulas de suma y diferencia de los cosenos para encontrar el coseno de la suma o diferencia de dos ángulos -
Cómo calcular el coseno de un ángulo -
Cómo calcular el seno de un ángulo -
Cómo utilizar SOHCAHTOA para encontrar las funciones trigonométricas de un triángulo rectángulo
¿Cómo trabajar con triángulos 45-45-90 grados Todos los triángulos 45-45-90 grado (también conocidos como 45ers) tienen lados que están en una relación única. Las dos piernas tienen la misma longitud exacta y la hipotenusa es que los tiempos de la longitud de la raíz cuadrada de 2. La…
Integrar una función utilizando el caso sine Cuando la función está integrando incluye un término de la forma (la2 - bx2)n, llamar su triángulo sustitución trigonométrica para el caso sinusoidal. Por ejemplo, supongamos que desea evaluar la siguiente integral:Este es un caso sinusoidal,…
Trabajar con razones trigonométricas en el plano de coordenadas Para poner los ángulos en el plano de coordenadas, esencialmente todo lo que hacemos es mirar las relaciones trigonométricas en términos de X y y valores en vez de frente, adyacente, y hipotenusa. Redefinición de estas proporciones para…
Aplicando el teorema de Pitágoras El teorema de Pitágoras se ha conocido durante al menos 2.500 años. Se utiliza el teorema de Pitágoras cuando se sabe las longitudes de dos lados de un triángulo rectángulo y quiere averiguar la longitud del tercer lado.El teorema de…
Geometría fórmulas y reglas para triángulos Las pirámides de tres ángulos, bidimensionales conocidos como triángulos son uno de los componentes básicos de la geometría (sin embargo de tres picos que sean). Triángulos, por supuesto, tienen sus propias fórmulas para encontrar el área y…
Problemas de la práctica de la geometría con triángulos y polígonos LA polígono es una figura geométrica que tiene al menos tres lados. El triángulo es el polígono más básico. Usted encontrará las siguientes fórmulas y propiedades útiles al responder a las preguntas que implican desigualdades triángulo,…
La identificación de triángulos por sus ángulos Se puede clasificar triángulos por sus ángulos, así como por sus lados. Las clasificaciones basadas en ángulos son como sigue:Triángulo aguda: Un triángulo con tres ángulos agudos (menos de 90 # 176-).Triángulo obtuso: Un triángulo con un…
La comparación de funciones seno y coseno en un gráfico La relación entre el coseno y seno gráficos es que el coseno es el mismo que el sine - solamente se desplaza a la izquierda en 90 grados, o pi-/ 2. La ecuación de trigonometría que representa esta relación esMira las gráficas de las funciones…
La determinación de si un objeto largo encaja en una esquina pasillo Aquí hay una aplicación de la trigonometría que puede muy bien ser capaz de relacionarse con: ¿Alguna vez ha tratado de conseguir un mueble grande en una esquina en una casa? Usted girar y girar y lo puso de punta, pero fue en vano. En este…
Dominios y rangos de funciones trigonométricas El dominio de una función se compone de todos los valores de entrada que una función puede manejar - la manera que la función está definida. Por supuesto, usted desea conseguir valores de salida (que conforman la gama) cuando introduce valores…
Gama de funciones seno y coseno de dominio y Las funciones seno y coseno son únicos en el mundo de las funciones trigonométricas, porque sus relaciones siempre tienen un valor. No importa desde qué ángulo lo de entrada, se obtiene una salida resultante. El valor que se obtiene puede ser 0,…
Seno y coseno identidades pitagóricas en un círculo unitario Si alguna vez se preguntó por qué la identidad de Pitágoras, el pecado2theta- + cos2theta- = 1, es tan importante, y de dónde viene, entonces sigue leyendo. Esta identidad es importante porque establece una expresión que involucra funciones…