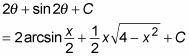Integrar una función utilizando el caso sine

Cuando la función está integrando incluye un término de la forma (la² - bx²)ⁿ, llamar su triángulo sustitución trigonométrica para el caso sinusoidal. Por ejemplo, supongamos que desea evaluar la siguiente integral:

Este es un caso sinusoidal, porque una constante menos un múltiplo de X² está siendo elevado a una potencia

He aquí cómo usted utiliza la sustitución trigonométrica para manejar el trabajo:

1. Dibuja el triángulo sustitución trigonométrica para el caso correcto.

   

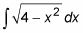
   Esta figura muestra cómo rellenar el triángulo para el caso de seno. Observe que el radical va en la adyacente lado del triángulo. Luego, para completar los otros dos lados del triángulo, utiliza las raíces cuadradas de los dos términos dentro del radical - es decir, 2 y X. Lugar 2 de la hipotenusa y X en el lado opuesto.

   Usted puede comprobar para asegurarse de que esta colocación es correcta utilizando el teorema de Pitágoras:

   

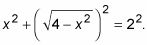
2. Identificar las piezas separadas de la integral (incluyendo dx) Que usted necesita expresar en términos de theta.

   En este caso, la función contiene dos piezas separadas que contienen X:

   

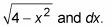
3. Exprese estas piezas en términos de funciones trigonométricas de theta.

   Este es el verdadero trabajo de trig sustitución, pero cuando su triángulo está configurado correctamente, este trabajo se hace mucho más fácil. En el caso de seno, todas funciones trigonométricas deben ser senos y cosenos.

   Para representar la parte radical como una función trigonométrica de theta, construir una primera fracción usando el radical

   

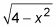
   como numerador y la constante de 2 como denominador. A continuación, establezca esta fracción igual a la función trigonométrica correspondiente:

   

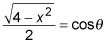
   Debido a que el numerador es el lado adyacente del triángulo y el denominador es la hipotenusa

   

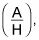
   esta fracción es igual a

   

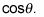
   Ahora un poco de álgebra recupera el radical sola en un lado de la ecuación:

   

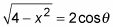
   Luego, si desea expresar dx como una función trigonométrica de theta. Para ello, construir otra fracción con la variable X en el numerador y la constante 2 en el denominador. A continuación, establezca esta fracción igual a la función trigonométrica correcta:

   

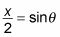
   Esta vez, el numerador es el lado opuesto del triángulo y el denominador es la hipotenusa

   

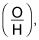
   por lo que esta fracción es igual a

   

   Ahora resolver X y luego diferenciar:

   

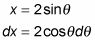
4. Vuelva a escribir la integral en términos de theta y evaluarla:

   

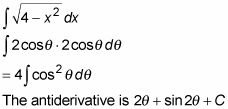
5. Para cambiar esos dos términos theta en X términos, la reutilización de la siguiente ecuación:

   

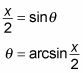
   Así que aquí está una sustitución que le da una respuesta:

   

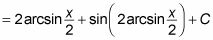
Esta respuesta es perfectamente válida para que, técnicamente hablando, puede parar aquí. Sin embargo, algunos profesores fruncir el ceño a la anidación de trig y funciones trigonométricas inversas, por lo que van a prefieren una versión simplificada de

Para saber esto, comenzar aplicando la fórmula del seno de doble ángulo para

Ahora usa tu triángulo sustitución trigonométrica para sustituir valores para

en términos de X:

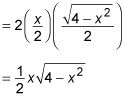
Para terminar, sustituir esta expresión para ese segundo término problemático para obtener su respuesta final en una forma simplificada: