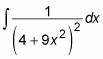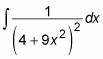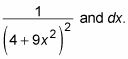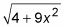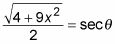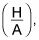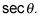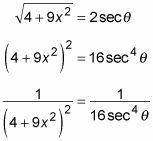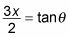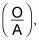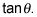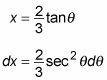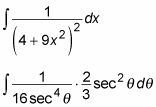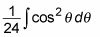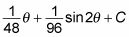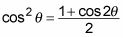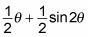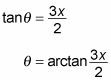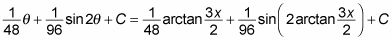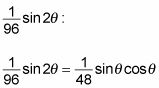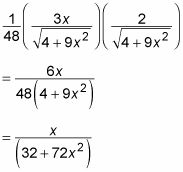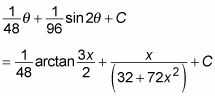Integrar una función utilizando el caso tangente
Cuando la función está integrando incluye un término de la forma (la2 + X2)n, llamar su trigonometría triángulo de sustitución para el caso tangente. Por ejemplo, supongamos que desea evaluar la siguiente integral:
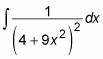
Este es un caso tangente, debido a una constante más un múltiplo de X2 está siendo elevado a una potencia (-2). He aquí cómo usted utiliza trig sustitución de integrar:
Dibuja el triángulo sustitución trigonométrica para el caso tangente.
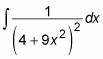
La figura muestra cómo rellenar el triángulo para el caso tangente. Observe que el radical de lo que hay dentro de los paréntesis va en la hipotenusa del triángulo. Luego, para completar los otros dos lados del triángulo, utilice las raíces cuadradas de los dos términos dentro del radical - es decir, 2 y 3X. Coloque el término constante 2 en el lado adyacente y el término variable de 3X en el lado opuesto.
Con el caso tangente, asegúrese de no mezclar su colocación de la variable y el constante.
Identificar las piezas separadas de la integral (incluyendo dx) Que usted necesita expresar en términos de theta.
En este caso, la función contiene dos piezas separadas que contienen X:
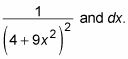
Exprese estas piezas en términos de funciones trigonométricas de theta.
En el caso de la tangente, todas funciones trigonométricas deben expresarse inicialmente como tangentes y secantes.
Para representar a la parte racional como una función trigonométrica de theta, construir una fracción usando el radical
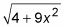
como numerador y la constante de 2 como denominador. A continuación, establezca esta fracción igual a la función trigonométrica correspondiente:
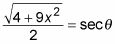
Debido a que esta fracción es la hipotenusa del triángulo sobre el lado adyacente
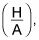
es igual a
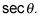
Ahora usa el álgebra y la trigonometría identidades para modificar esta ecuación en forma:
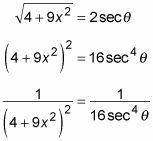
A continuación, expresar dx como una función trigonométrica de theta. Para ello, construir otra fracción con la variable 3X en el numerador y la constante 2 en el denominador:
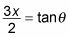
Esta vez, la fracción es el lado opuesto del triángulo sobre el lado adyacente
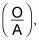
por lo que es igual
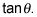
Ahora resolver X y luego diferenciar:
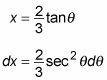
Expresar la integral en términos de theta y evaluarla:
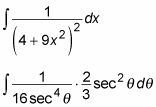
Ahora, algunos de cancelación y reorganización convierte esta integral en algo manejable de aspecto desagradable:
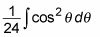
En este punto, usted puede evaluar esta integral:
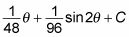
Así que aquí está la sustitución:
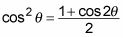
Y aquí está la primitiva:
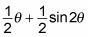
Cambie los dos términos theta de nuevo en X términos:
Usted necesita encontrar una manera de expresar theta en términos de X. Aquí está la forma más sencilla:
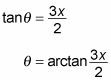
Así que aquí está una sustitución que le da una respuesta:
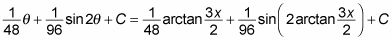
Esta respuesta es válida, pero la mayoría de los profesores no estará loco por ese segundo mandato feo, con el seno de un arco tangente. Para simplificarlo, aplicar la fórmula del seno de doble ángulo para
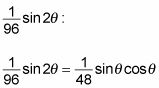
Ahora usa tu triángulo sustitución trigonométrica para sustituir valores para

en términos de X:
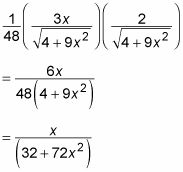
Por último, utilizar este resultado para expresar la respuesta en términos de X:
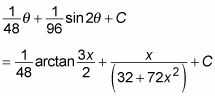
Sobre el autor
 Cómo utilizar la sustitución tangente a integrar
Cómo utilizar la sustitución tangente a integrar Con el método de sustitución trigonométrica, puede hacerlo integrales contienen radicales de las siguientes formas:dónde la es una constante y u es una expresión que contiene X.Usted va a encantar esta técnica # 133- tanto como pegar un hierro…
 Cómo utilizar la sustitución trigonométrica para integrar
Cómo utilizar la sustitución trigonométrica para integrar Con el método de sustitución trigonométrica, puede hacerlo integrales que contienen radicales de las siguientes formas (dada la es una constante y u es una expresión que contiene X):Usted va a encantar esta técnica ... casi tanto como pegar un…
 Cómo utilizar la sustitución trigonométrica para integrar los radicales de la forma sinusoidal
Cómo utilizar la sustitución trigonométrica para integrar los radicales de la forma sinusoidal Antes de leer este artículo, usted debe comprobar fuera de la discusión de la sustitución trigonométrica en el artículo complementario, " Cómo utilizar Trig Sustitución de integrar ".Con el método de sustitución trigonométrica, puede…
 Integrar una función utilizando el caso secante
Integrar una función utilizando el caso secante Cuando la función que se está integrando incluye un término de la forma (bx2 - la2)n, llamar su triángulo sustitución trigonométrica para el caso secante. Por ejemplo, suponga que desea evaluar esta integral:Este es un caso secante, debido a…
 Integrar una función utilizando el caso sine
Integrar una función utilizando el caso sine Cuando la función está integrando incluye un término de la forma (la2 - bx2)n, llamar su triángulo sustitución trigonométrica para el caso sinusoidal. Por ejemplo, supongamos que desea evaluar la siguiente integral:Este es un caso sinusoidal,…
 Trabajar con razones trigonométricas en el plano de coordenadas
Trabajar con razones trigonométricas en el plano de coordenadas Para poner los ángulos en el plano de coordenadas, esencialmente todo lo que hacemos es mirar las relaciones trigonométricas en términos de X y y valores en vez de frente, adyacente, y hipotenusa. Redefinición de estas proporciones para…
 Sine Express en términos de coseno
Sine Express en términos de coseno A pesar de que cada función de la trigonometría es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener…
 Sine Express en términos de secante o cosecante
Sine Express en términos de secante o cosecante A pesar de que cada función trigonométrica es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener algunos…
 Sine Express en términos de cotangente
Sine Express en términos de cotangente A pesar de que cada función de la trigonometría es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener…
 Sine Express en términos de la tangente
Sine Express en términos de la tangente A pesar de que cada función de la trigonometría es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener…
 ¿Cómo encontrar identidades medio-ángulo para tangente
¿Cómo encontrar identidades medio-ángulo para tangente La media de ángulo trig identidad para tangente tiene dos versiones. En lugar de que esto sea una molestia, que tiene más de una opción es realmente bastante agradable, porque se puede elegir la versión que mejor se adapte a su situación. Las…
 ¿Cómo resolver funciones trigonométricas inversas con ángulos poco comunes
¿Cómo resolver funciones trigonométricas inversas con ángulos poco comunes Cuando se trabaja con funciones trigonométricas inversas, siempre es más conveniente cuando los números que está trabajando son los resultados de la aplicación de una de las funciones trigonométricas a una medida de ángulo común. Cuando el…