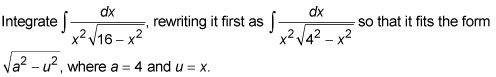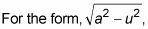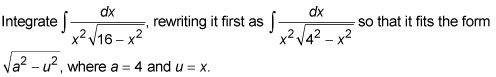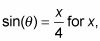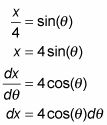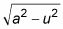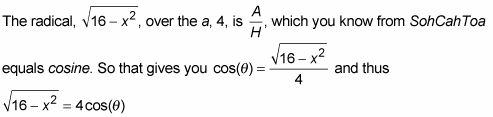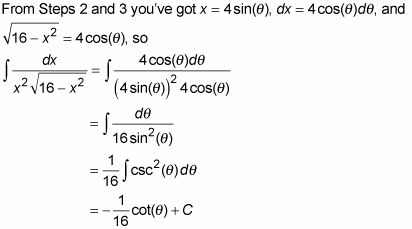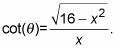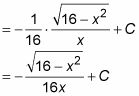Cómo utilizar la sustitución trigonométrica para integrar los radicales de la forma sinusoidal
Antes de leer este artículo, usted debe comprobar fuera de la discusión de la sustitución trigonométrica en el artículo complementario, " Cómo utilizar Trig Sustitución de integrar ".
Con el método de sustitución trigonométrica, puede hacerlo integrales contienen radicales de las siguientes formas:
Este artículo se refiere a la primera forma que usted aborda con la función seno. Las otras dos formas se manejan con la tangente y funciones secantes y se discuten en otros artículos.
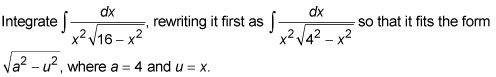
Dibuja un triángulo rectángulo donde
Usted debe confirmar esto con el teorema de Pitágoras.
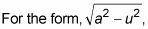
la siguiente figura muestra una SOHCAHTOA triángulo.
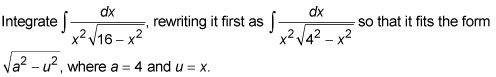
Resolver
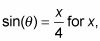
entonces diferenciar y resolver dx.
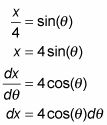
Encuentra que la función trigonométrica es igual al radical sobre el la (Eso es la de
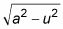
no la como en adyacente), Y luego resolver el radical.
Mira el triángulo en la figura.
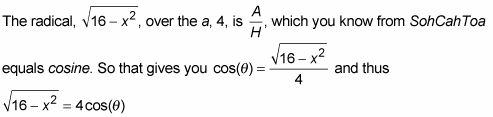
Utilizar los resultados de los pasos 2 y 3 para hacer sustituciones en el problema original y luego integrar.
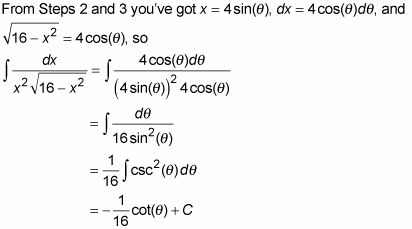
El triángulo muestra que
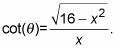
Así que sustituir parte posterior para su respuesta final:
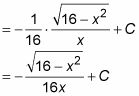
Es un paseo por el parque.
-
Cómo calcular un ángulo utilizando funciones trigonométricas inversas -
¿Cómo integrar potencias pares de secantes con tangentes -
¿Cómo integrar potencias impares de tangentes con secantes -
¿Cómo integrar potencias impares de senos y cosenos -
¿Cómo integrar los problemas de seno / coseno con una potencia extraña, positivo de seno -
¿Cómo integrar los problemas de seno / coseno con una potencia extraña, positivo de coseno
¿Cómo integrar tangentes / problemas secantes con una potencia extraña, positivo de la tangente He aquí cómo usted integra un integrante trig que contiene tangentes y secantes donde el poder tangente es impar y positivo. Usted necesitará la versión tangente secante de la identidad de Pitágoras:Lop fuera un factor secante-tangente y…
¿Cómo resolver integrales con la sustitución de variables En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.Declare una…
Cómo utilizar la sustitución de seno para integrar Con el método de sustitución trigonométrica, puede hacerlo integrales que contienen radicales de ciertas formas, ya que coinciden con las funciones trigonométricas. Un seno puede tomar el lugar de un resto en una forma particular.Dibuja un…
Cómo utilizar SOHCAHTOA para encontrar las funciones trigonométricas de un triángulo rectángulo El estudio de la trigonometría comienza con el triángulo rectángulo. Las tres funciones principales trigonométricas (seno, coseno y tangente) y sus inversos (cosecante, secante y cotangente) todo lo que dicen algo acerca de las longitudes de los…
Cómo utilizar la sustitución tangente a integrar Con el método de sustitución trigonométrica, puede hacerlo integrales contienen radicales de las siguientes formas:dónde la es una constante y u es una expresión que contiene X.Usted va a encantar esta técnica # 133- tanto como pegar un hierro…
Cómo utilizar la sustitución trigonométrica para integrar Con el método de sustitución trigonométrica, puede hacerlo integrales que contienen radicales de las siguientes formas (dada la es una constante y u es una expresión que contiene X):Usted va a encantar esta técnica ... casi tanto como pegar un…
Integrar una función utilizando el caso secante Cuando la función que se está integrando incluye un término de la forma (bx2 - la2)n, llamar su triángulo sustitución trigonométrica para el caso secante. Por ejemplo, suponga que desea evaluar esta integral:Este es un caso secante, debido a…
Integrar una función utilizando el caso sine Cuando la función está integrando incluye un término de la forma (la2 - bx2)n, llamar su triángulo sustitución trigonométrica para el caso sinusoidal. Por ejemplo, supongamos que desea evaluar la siguiente integral:Este es un caso sinusoidal,…
Integrar una función utilizando el caso tangente Cuando la función está integrando incluye un término de la forma (la2 + X2)n, llamar su trigonometría triángulo de sustitución para el caso tangente. Por ejemplo, supongamos que desea evaluar la siguiente integral:Este es un caso tangente,…
Saber cuando para evitar la sustitución de la trigonometría Es útil saber cuándo debe evitar el uso de la sustitución trigonométrica. Con algunas integrales, es mejor ampliar el problema en un polinomio. Por ejemplo, mira la siguiente integral:Esto puede parecer un buen lugar para utilizar la…
Aplicando el teorema de Pitágoras El teorema de Pitágoras se ha conocido durante al menos 2.500 años. Se utiliza el teorema de Pitágoras cuando se sabe las longitudes de dos lados de un triángulo rectángulo y quiere averiguar la longitud del tercer lado.El teorema de…
La identificación de la 45 - triángulo de 90 grados - 45 Un 45 a 45 - 90 grados triángulo (o triángulo rectángulo isósceles) es un triángulo con ángulos de 45 # 176-, 176- 45 # y 90 # 176- y los lados de la relación entreTenga en cuenta que se trata de la forma de la mitad de un cuadrado, corte a…