¿Cómo integrar tangentes / problemas secantes con una potencia extraña, positivo de la tangente
He aquí cómo usted integra un integrante trig que contiene tangentes y secantes donde el poder tangente es impar y positivo. Usted necesitará la versión tangente secante de la identidad de Pitágoras:
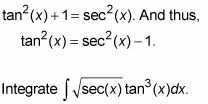
Lop fuera un factor secante-tangente y moverlo a la derecha.
En primer lugar, reescribir el problema:

Convertir los restantes (incluso) tangentes a secantes con la versión tangente secante de la identidad de Pitágoras.

Ahora hacer el cambio.
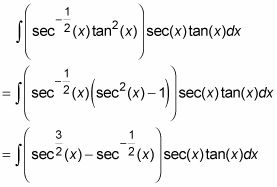
Resolver con el método de sustitución con u = S (X) Y du = S (X) Tan (X)dx.
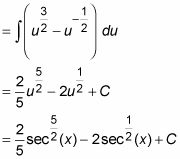
-
 ¿Cómo integrar potencias pares de secantes con tangentes
¿Cómo integrar potencias pares de secantes con tangentes -
 ¿Cómo integrar potencias impares de tangentes con secantes
¿Cómo integrar potencias impares de tangentes con secantes -
 ¿Cómo integrar los problemas de seno / coseno con una potencia extraña, positivo de seno
¿Cómo integrar los problemas de seno / coseno con una potencia extraña, positivo de seno -
 ¿Cómo integrar tangentes / problemas secantes con un par, el poder positivo de la secante
¿Cómo integrar tangentes / problemas secantes con un par, el poder positivo de la secante -
 ¿Cómo integrar los problemas de seno / coseno con una potencia extraña, positivo de coseno
¿Cómo integrar los problemas de seno / coseno con una potencia extraña, positivo de coseno -
 ¿Cómo integrar los problemas con un par, el poder positivo de la tangente
¿Cómo integrar los problemas con un par, el poder positivo de la tangente
La geometría no es todo acerca de ángulos puntiagudos - hay círculos, también. Lo interesante de los círculos no es sólo su redondez: Familiarizarse con las fórmulas de la geometría que le ayudan a medir los ángulos alrededor de círculos,…
Una línea es tangente a un círculo si toca al uno y sólo un punto. Si una línea es tangente a un círculo, entonces es perpendicular al radio trazado hasta el punto de tangencia. Echa un vistazo a las ruedas de la bicicleta en la siguiente…
Un ángulo que cruza un círculo puede tener su vértice en el interior, sobre o fuera del círculo. Este artículo aborda los tres tipos de ángulos que tienen sus vértices fuera de un círculo: ángulos secante-secantes, ángulos…
Puede utilizar el secante-secante Poder teorema para resolver algunos problemas de círculo. Este teorema implica - ¿Estás sentado abajo - dos secantes! (Si usted está tratando de llegar a un nombre creativo para su hijo como Dweezil o Unidad…
Puede resolver algunos problemas de círculo utilizando el Poder Teorema Tangente-secante. Este teorema afirma que si una tangente y una secante se han extraído de un punto externo a un círculo, entonces el cuadrado de la medida de la tangente es…
Usted muestra el diámetro y el radio de un círculo dibujando segmentos a partir de un punto en el círculo, ya sea hacia oa través del centro del círculo. Sin embargo, otras dos figuras rectas tienen un lugar en un círculo. Una de estas figuras…
Las funciones cosecante y secante están estrechamente ligados a seno y coseno, porque son los respectivos recíprocos. En referencia al plano de coordenadas, cosecante es r/y, y secante es r/X. El valor de r es la longitud de la hipotenusa de un…
La tangente y cotangente están relacionadas no sólo por el hecho de que son recíprocos, sino también por el comportamiento de sus rangos. En referencia al plano de coordenadas, tangente es y/X, y cotangente es X/y. Los dominios de ambas…
A pesar de que cada función de la trigonometría es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener…
A pesar de que cada función de la trigonometría es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener…
En trigonometría, valores tangentes van desde menos infinito hasta el infinito positivo. Así que cuando usted multiplica toda la función tangente de un número, esto es lo que sucede: Si se multiplica por un número mayor que 1, la función se…
En trigonometría, multiplicando el ángulo variable en una función tangente tiene el mismo efecto como lo hace con funciones seno y coseno - que afecta el periodo de la función. Si el múltiplo es 2, como en y = Tan 2X, a continuación, la…
