Cómo una tangente se refiere a un círculo
Una línea es tangente a un círculo si toca al uno y sólo un punto. Si una línea es tangente a un círculo, entonces es perpendicular al radio trazado hasta el punto de tangencia. Echa un vistazo a las ruedas de la bicicleta en la siguiente figura.
En esta figura, las ruedas son, por supuesto, los círculos, los radios son radios, y el suelo es un línea tangente. El punto en el que cada rueda toca el suelo es un punto de tangencia. Y lo más importante - lo que el teorema que dice - es que el radio que va al punto de tangencia es perpendicular a la línea tangente.
No se olviden de revisar problemas círculo de líneas tangentes y los ángulos rectos que se producen en los puntos de tangencia. Puede que tenga que dibujar en una o más radios a los puntos de tangencia para crear los ángulos rectos. Los ángulos rectos a menudo se convierten en partes de triángulos rectángulos (oa veces rectángulos).
Aquí hay un problema de ejemplo: Encontrar el radio del círculo C y la longitud del segmento DE en la siguiente figura.
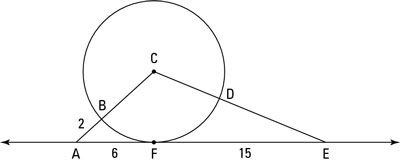
Cuando usted ve un problema círculo, usted debe estar diciendo a ti mismo: radios, radios, radios!
Así que el radio es 8. Entonces usted puede ver ese triángulo CFE es un triángulo 08/15/17, por lo CE es 17. (Por supuesto, también se puede obtener CE con el Teorema de Pitágoras.) CD es 8 (y es el tercer radio en este problema- hace radios, radios, radios ¿sonar una campana?). Por Consiguiente, DE es 17-8 ó 9. Eso lo hace.
-
Dibuja círculos y tangentes en una TI-83 Plus gráfico -
Ocultar y eliminar objetos en jr Cabri. -
Añadir una línea tangente a un gráfico en TI-Nspire -
Conceptos de geometría a su estudiante de la escuela secundaria deben conocer las normas básicas comunes -
¿Cómo medir los círculos -
¿Cómo encontrar las líneas tangentes de una parábola que pasan por un punto determinado
Cómo determinar la medida de un ángulo cuyo vértice se encuentra fuera de un círculo Un ángulo que cruza un círculo puede tener su vértice en el interior, sobre o fuera del círculo. Este artículo aborda los tres tipos de ángulos que tienen sus vértices fuera de un círculo: ángulos secante-secantes, ángulos…
Cómo determinar la medida de un ángulo cuyo vértice está en un círculo De los tres lugares vértice de un ángulo puede estar en relación con un círculo (dentro, sobre o fuera del círculo), los dos tipos de ángulos que tienen su vértice en un círculo - inscrito ángulos y ángulos tangente-acordes - son los que…
Cómo identificar radios, acordes, y diámetros Cuando se trabaja con los círculos, hay tres componentes en línea recta que tiene que ser capaz de identificar: radios, acordes, y diámetros.Radio: El radio de un círculo - la distancia desde su centro a un punto en el círculo - le dice el…
¿Cómo resolver un problema-tangente común los problema-tangente común se nombra para el segmento única tangente que es tangente a dos círculos. Su objetivo es encontrar la longitud de la tangente. Estos problemas son un poco complicado, pero deben hacer que poca dificultad si se utiliza…
Cómo utilizar radios extra para resolver un problema Al comprar una casa, las tres cosas más importantes a considerar son localización, localización, localización. Con los círculos, es radios, radios, radios. En los problemas de círculo, a menudo es necesario añadir radios extra y radios…
Cómo utilizar el teorema de poder secante-secante Puede utilizar el secante-secante Poder teorema para resolver algunos problemas de círculo. Este teorema implica - ¿Estás sentado abajo - dos secantes! (Si usted está tratando de llegar a un nombre creativo para su hijo como Dweezil o Unidad…
Cómo utilizar el teorema de la energía-tangente secante Puede resolver algunos problemas de círculo utilizando el Poder Teorema Tangente-secante. Este teorema afirma que si una tangente y una secante se han extraído de un punto externo a un círculo, entonces el cuadrado de la medida de la tangente es…
Estrategias de prueba en la geometría Saber cómo escribir pruebas de geometría de dos columnas proporciona una base sólida para trabajar con teoremas. La práctica de estas estrategias le ayudará a escribir las pruebas de geometría fácilmente en poco tiempo:Hacer un plan de juego.…
Estrategias Prueba resumen Las siguientes estrategias pueden ayudarle mucho cuando estás trabajando en pruebas de geometría de dos columnas. Usted debe revisar estas estrategias y practicar el uso de ellos hasta que se convierten internalizada. Estas estrategias le hará…
Evaluando el área de un polígono No sólo pueden polígonos pueden clasificar por el número de lados que tienen y por sus ángulos, pero también pueden ser agrupados de acuerdo a algunas de sus cualidades. Los polígonos pueden tener tres características de la personalidad:…
Ángulos en un círculo Hay varias maneras de dibujo un ángulo en un círculo, y cada uno tiene una forma especial de calcular el tamaño de ese ángulo. Cuatro tipos diferentes de ángulos son: central, inscrito, interior, y exterior. Aquí, verá ejemplos de estos…
Acordes frente tangentes de los círculos Usted muestra el diámetro y el radio de un círculo dibujando segmentos a partir de un punto en el círculo, ya sea hacia oa través del centro del círculo. Sin embargo, otras dos figuras rectas tienen un lugar en un círculo. Una de estas figuras…