¿Cómo encontrar las líneas tangentes de una parábola que pasan por un punto determinado
¿Alguna vez quiso determinar la ubicación de una línea a través de un punto dado que es tangente a una curva dada? Por supuesto que tienes! He aquí cómo lo haces.
Determinar los puntos de tangencia de las líneas por el punto (1, -1) que son tangentes a la parábola
Si representa la parábola y trazar el punto, se puede ver que hay dos maneras de dibujar una línea que pasa por (1, -1) y es tangente a la parábola: hasta la derecha y de arriba a la izquierda (se muestra en la la figura).
La clave de este problema está en el significado de la derivada: La derivada de una función en un punto dado es la pendiente de la recta tangente en ese punto. Por lo tanto, sólo hay que establecer la derivada de la parábola igual a la pendiente de la recta tangente y resolver:
Debido a que la ecuación de la parábola es
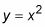
usted puede tomar un punto general de la parábola, (X, y) Y sustituto
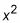
para y.
Tome la derivada de la parábola.
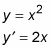
Utilizando la fórmula de la pendiente, ajuste la pendiente de cada recta tangente a partir de (1, -1) para
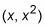
igual a la derivada en
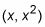
que es 2X, y resuelve para X.
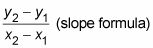
Por cierto, los cálculos que se hace en este paso puede tener más sentido para usted si usted piensa en él como la aplicación de una de las líneas tangentes - dice el que va a la derecha - pero la matemática en realidad se aplica tanto a líneas tangentes simultáneamente.
Entonces el X-coordenadas de los puntos de tangencia están
Conecte cada uno de ellos X-coordina en
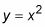
para obtener el y-coordenadas.
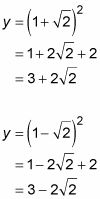
Por lo tanto, los dos puntos de tangencia están
-
Dibuja círculos y tangentes en una TI-83 Plus gráfico -
Encuentra la pendiente de una curva con la TI-84 Plus -
Añadir una línea tangente a un gráfico en TI-Nspire -
Encontrar las intersecciones de las líneas y las parábolas -
Cómo graficar parábolas -
Calcular la pendiente de una función utilizando el cociente de diferencias
Cómo determinar el costo marginal, el ingreso marginal y el beneficio marginal en la economía El costo marginal, el ingreso marginal y beneficio marginal todos implican la cantidad de una función sube (o hacia abajo) a medida que avanza más de 1 hacia la derecha - esto es muy similar a la forma en que las obras de aproximación…
¿Cómo encontrar una línea normal a una curva Una línea normal a una curva en un punto dado es la línea perpendicular a la línea que es tangente en ese mismo punto. Encontrar los puntos de perpendicularidad para todas las líneas normales a la parábolaque pasan por el punto (3,…
¿Cómo encontrar una línea normal perpendicular a una recta tangente Una línea normal a una curva en un punto dado es la línea perpendicular a la línea que es tangente en ese mismo punto. Encontrar los puntos de perpendicularidad para todas las líneas normales a la parábolaque pasan por el punto (3,…
¿Cómo encontrar los números críticos de una función Todos los extremos locales se producen en los puntos críticos de una función - que es donde la derivada es cero o indefinido (pero no se olvide que los puntos críticos no siempre son extremos locales). Así, el primer paso en la búsqueda de…
¿Cómo encontrar la derivada de una curva de El cálculo es la matemática de cambio - lo que necesita saber cómo encontrar la derivada de una parabolla, que es una curva con una pendiente constante cambio.La siguiente figura muestra la gráfica de la parábola anterior.Observe cómo la…
Cómo representar gráficamente una parábola horizontal Una parábola horizontal cuenta con sus propias ecuaciones para encontrar su partes- estos son sólo un poco diferente en comparación con una parábola vertical. La distancia al foco y la directriz desde el vértice en este caso es horizontal,…
Cómo representar gráficamente una parábola vertical, Con el fin de representar gráficamente una parábola correctamente, es importante tener en cuenta si es una horizontal o una parábola vertical. Esto es porque mientras que las variables y constantes en las ecuaciones para las dos curvas tienen el…
¿Cómo saber cuando un derivado no existe Hay tres situaciones en las que un derivado de falla de existir. La derivada de una función en un punto dado es la pendiente de la recta tangente en ese punto. Por lo tanto, si no se puede trazar una línea tangente, no hay derivada - que sucede en…
Cómo hacer aproximaciones lineales Debido a que las funciones ordinarias son localmente lineal (que significa recto) - y cuanto más te acercas a ellos, el más recto que buscar-una línea tangente a una función es una buena aproximación de la función cerca del punto de…
El cociente de diferencias: el puente entre el álgebra (pendiente) y el cálculo (la derivada) Una de las piedras angulares de cálculo es el cociente de diferencias. El cociente de diferencias - junto con los límites - le permite tomar la fórmula pendiente edad ordinaria que utilizó para calcular la pendiente de las líneas en la clase de…
Cómo una tangente se refiere a un círculo Una línea es tangente a un círculo si toca al uno y sólo un punto. Si una línea es tangente a un círculo, entonces es perpendicular al radio trazado hasta el punto de tangencia. Echa un vistazo a las ruedas de la bicicleta en la siguiente…
Cómo determinar la medida de un ángulo cuyo vértice se encuentra fuera de un círculo Un ángulo que cruza un círculo puede tener su vértice en el interior, sobre o fuera del círculo. Este artículo aborda los tres tipos de ángulos que tienen sus vértices fuera de un círculo: ángulos secante-secantes, ángulos…