Cómo representar gráficamente una parábola vertical,
Con el fin de representar gráficamente una parábola correctamente, es importante tener en cuenta si es una horizontal o una parábola vertical. Esto es porque mientras que las variables y constantes en las ecuaciones para las dos curvas tienen el mismo propósito, su efecto en los gráficos en el final es un poco diferente.
Conteúdo
Una parábola vertical tiene su eje de simetría en X = h, y el vértice es (h, v). Con esta información, usted puede encontrar el foco y la directriz.
El enfoque es la distancia desde el vértice al foco es 1 / (4la), dónde la se pueden encontrar en la ecuación de la parábola (que es el escalar en frente de los paréntesis). El enfoque, como un punto, es (h, v + 1 / (4la)) - Debe ser directamente por encima o directamente debajo del vértice. Siempre aparece dentro de la parábola.
La ecuación de la directriz es y = v - 1 / (4la). Debe ser la misma distancia desde el vértice a lo largo del eje de simetría como el foco, en la dirección opuesta. La directriz aparece fuera de la parábola y es perpendicular al eje de simetría. Debido a que el eje de simetría es vertical, la directriz es una de línea horizontal por lo tanto, tiene una ecuación de la forma y = la constante, que es v - 1 / (4la).
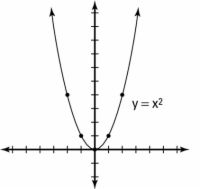  Agrandar1 Cuadrar las variables en la ecuación de la parábola.La cuadratura de las variables en la ecuación de la parábola determina dónde se abre: Cuando el X se eleva al cuadrado y y no lo es, el eje de simetría es vertical y la parábola se abre hacia arriba o hacia abajo. Por ejemplo, y = X2 es un parabola- vertical de su gráfica se muestra. | 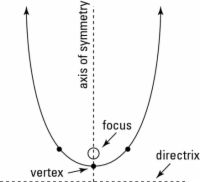 Agrandar2 Encaja con coeficientes negativos en parábolas.Sea consciente de coeficientes negativos en parábolas. Si la parábola es vertical, un coeficiente negativo hará que la parábola abierta hacia abajo. La figura puede ser referido como el " martini " de parábolas. La gráfica se ve como un vaso de martini: El eje de simetría es el vástago de vidrio, la directriz es la base de la copa, y el enfoque es el de oliva. Usted necesita todas esas partes para hacer un buen martini y una parábola. | 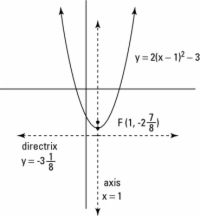 Agrandar3 Encuentra las piezas de la parábola y crear parábola vertical.Por ejemplo, la ecuación y = 2 (X - 1)2 - 3, tiene su vértice en (1, -3). Esto significa eso la = 2, h = 1, y v = -3. Con esta información, se puede identificar todas las partes de una parábola (eje de simetría, el enfoque, y la directriz) como puntos o ecuaciones: En primer lugar, encontrar el eje de simetría. El eje de simetría está en X = h, Lo que significa que X = 1. En segundo lugar, determinar la distancia focal y escribir el foco como un punto. Puede encontrar la distancia focal mediante el uso de la fórmula 1 / (4la). Porque la = 2, la distancia focal de esta parábola es octavo. Con esta distancia, se puede escribir el enfoque como el punto (h,v + 1.4la), O (1, -2-7/8) En tercer lugar, encontrar la directriz. Puede utilizar la ecuación de la directriz: y = v - 1.4la, o y = -3-1 / 8. Por último, la gráfica de la parábola y etiquetar todas sus partes como se muestra. Siempre es una buena idea para trazar al menos otros dos puntos, además del vértice para que pueda demostrar que su transformación vertical es correcta. Debido a que la transformación vertical en esta ecuación es un factor de 2, los dos puntos en ambos lados del vértice se estiran en un factor de dos. Así, desde el vértice, se traza un punto que es el más adecuado, y hasta dos (en lugar de uno). A continuación, puede dibujar el mismo punto en el otro lado del eje de Simetría los otros dos puntos en la gráfica están en (2, -1) y (0, -1). |
Gráficas y funciones de transformación Puede graficar funciones bastante cómodamente utilizando una calculadora gráfica, pero se le frustró el uso de esta tecnología, si usted no tiene una buena idea de lo que vas a encontrar y donde usted lo encontrará. Usted necesita tener una…
¿Cómo encontrar una línea normal a una curva Una línea normal a una curva en un punto dado es la línea perpendicular a la línea que es tangente en ese mismo punto. Encontrar los puntos de perpendicularidad para todas las líneas normales a la parábolaque pasan por el punto (3,…
¿Cómo encontrar las líneas tangentes de una parábola que pasan por un punto determinado ¿Alguna vez quiso determinar la ubicación de una línea a través de un punto dado que es tangente a una curva dada? Por supuesto que tienes! He aquí cómo lo haces.Determinar los puntos de tangencia de las líneas por el punto (1, -1) que son…
Cómo representar gráficamente una parábola horizontal Una parábola horizontal cuenta con sus propias ecuaciones para encontrar su partes- estos son sólo un poco diferente en comparación con una parábola vertical. La distancia al foco y la directriz desde el vértice en este caso es horizontal,…
Cálculo: cómo representar gráficamente una elipse Una elipse es básicamente un círculo que ha sido aplastado, ya sea horizontal o verticalmente. Desde una perspectiva de pre-cálculo, un elipse es un conjunto de puntos en un plano, la creación de un óvalo, forma curvada de tal manera que la…
Cómo graficar una elipse Un elipse es un conjunto de puntos en un plano, la creación de un óvalo, forma curvada, de tal manera que la suma de las distancias desde cualquier punto de la curva a dos puntos fijos (la focos) Es una constante (siempre la misma). Una elipse es…
Cómo graficar funciones parentales En matemáticas, se ve ciertos gráficos una y otra vez. Por esa razón, estas, funciones comunes originales se llaman gráficos de los padres, e incluyen gráficas de funciones cuadráticas, raíces cuadradas, valores absolutos, cúbicas y raíces…
Cómo identificar las cuatro secciones cónicas en forma de ecuación Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…
Cómo identificar el mínimo y máximo en parábolas verticales Parábolas verticales dan una pieza importante de información: Cuando la parábola se abre hacia arriba, el vértice es el punto más bajo en el gráfico - llamado el mínimo, o min. Cuando la parábola se abre hacia abajo, el vértice es el punto…
Cómo identificar las cuatro secciones cónicas en forma de gráfico Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…
Truco Ley para cuadráticas: cómo encontrar rápidamente la ubicación del vértice de una parábola Para ahorrar tiempo al graficar una función cuadrática en la prueba ACT de matemáticas, puede encontrar rápidamente la ubicación del vértice de la parábola en relación con el y-eje. Sólo tienes que utilizar el siguiente truco sencillo…
Truco Ley para cuadráticas: cómo encontrar rápidamente la dirección de una parábola Para ahorrar tiempo al graficar una función cuadrática en la prueba ACT de matemáticas, puede determinar rápidamente la dirección de la parábola usando un simple truco basado en el coeficiente la.Este truco se relaciona con el signo de la…