Truco Ley para cuadráticas: cómo encontrar rápidamente la ubicación del vértice de una parábola
Para ahorrar tiempo al graficar una función cuadrática en la prueba ACT de matemáticas, puede encontrar rápidamente la ubicación del vértice de la parábola en relación con el y-eje. Sólo tienes que utilizar el siguiente truco sencillo basado en las variables la y b (en los términos hacha2 y bx):
Cuando los signos de la y b son los mismos (ya sea positiva o tanto ambos negativos), los cambios gráfica de la izquierda. Es decir, el vértice de la parábola es a la izquierda de la y-eje.
Cuando los signos de la y b son diferentes (uno es positivo y el otro es negativo), los cambios de gráfica de la derecha. En este caso, el vértice de la parábola es a la derecha de la y-eje.
Una buena regla mnemotécnica para recordar esta regla es que la palabra mismo y la palabra izquierda ambos tienen cuatro letras.
Ejemplo
Una función cuadrática y = hacha2 + bx + c cruza la X eje a X = 4 y X = -2. Cuál de los siguientes debe ser verdad?
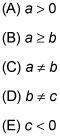
A primera vista, se puede pensar que esta difícil cuestión ni siquiera es responsable. Un bosquejo rápido que muestra que una gran cantidad de diferentes parábolas podría encajar esta descripción:
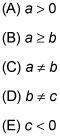
Lo único que se sabe con certeza es que el vértice de la parábola es horizontal en el medio de estos dos puntos, por lo que es en algún lugar de la línea X = 1. Por lo tanto, la parábola (lo que parece a) se desplaza hacia la derecha, por lo la y b tienen diferentes signos. Así la no es igual b, haciendo que la opción de respuesta correcta (C).
-
Cómo construir objetos geométricos en la TI-Nspire -
Para ajustar manualmente la configuración de la ventana cuando la representación gráfica -
Curvas Crossing: encontrar las intersecciones de parábolas y círculos -
Encontrar las intersecciones de las líneas y las parábolas -
Cómo graficar parábolas -
Cómo multiplicar y dividir números positivos y negativos
Gráficas y funciones de transformación Puede graficar funciones bastante cómodamente utilizando una calculadora gráfica, pero se le frustró el uso de esta tecnología, si usted no tiene una buena idea de lo que vas a encontrar y donde usted lo encontrará. Usted necesita tener una…
¿Cómo encontrar una línea normal a una curva Una línea normal a una curva en un punto dado es la línea perpendicular a la línea que es tangente en ese mismo punto. Encontrar los puntos de perpendicularidad para todas las líneas normales a la parábolaque pasan por el punto (3,…
¿Cómo encontrar el área con la versión de acceso directo del teorema fundamental del cálculo El teorema fundamental del cálculo tiene una versión de acceso directo que hace que encontrar el área bajo una curva en un instante. Aquí está. Dejar F ser cualquier antiderivada de la función F- despuésCon esta versión del teorema…
¿Cómo encontrar una línea normal perpendicular a una recta tangente Una línea normal a una curva en un punto dado es la línea perpendicular a la línea que es tangente en ese mismo punto. Encontrar los puntos de perpendicularidad para todas las líneas normales a la parábolaque pasan por el punto (3,…
¿Cómo encontrar las líneas tangentes de una parábola que pasan por un punto determinado ¿Alguna vez quiso determinar la ubicación de una línea a través de un punto dado que es tangente a una curva dada? Por supuesto que tienes! He aquí cómo lo haces.Determinar los puntos de tangencia de las líneas por el punto (1, -1) que son…
Cómo representar gráficamente una parábola horizontal Una parábola horizontal cuenta con sus propias ecuaciones para encontrar su partes- estos son sólo un poco diferente en comparación con una parábola vertical. La distancia al foco y la directriz desde el vértice en este caso es horizontal,…
Cómo representar gráficamente una parábola vertical, Con el fin de representar gráficamente una parábola correctamente, es importante tener en cuenta si es una horizontal o una parábola vertical. Esto es porque mientras que las variables y constantes en las ecuaciones para las dos curvas tienen el…
Cómo graficar funciones parentales En matemáticas, se ve ciertos gráficos una y otra vez. Por esa razón, estas, funciones comunes originales se llaman gráficos de los padres, e incluyen gráficas de funciones cuadráticas, raíces cuadradas, valores absolutos, cúbicas y raíces…
Cómo identificar las cuatro secciones cónicas en forma de ecuación Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…
Cómo identificar el mínimo y máximo en parábolas verticales Parábolas verticales dan una pieza importante de información: Cuando la parábola se abre hacia arriba, el vértice es el punto más bajo en el gráfico - llamado el mínimo, o min. Cuando la parábola se abre hacia abajo, el vértice es el punto…
Cómo determinar la medida de un ángulo cuyo vértice se encuentra fuera de un círculo Un ángulo que cruza un círculo puede tener su vértice en el interior, sobre o fuera del círculo. Este artículo aborda los tres tipos de ángulos que tienen sus vértices fuera de un círculo: ángulos secante-secantes, ángulos…
Truco Ley para cuadráticas: cómo encontrar rápidamente la dirección de una parábola Para ahorrar tiempo al graficar una función cuadrática en la prueba ACT de matemáticas, puede determinar rápidamente la dirección de la parábola usando un simple truco basado en el coeficiente la.Este truco se relaciona con el signo de la…