Cómo identificar el mínimo y máximo en parábolas verticales
Parábolas verticales dan una pieza importante de información: Cuando la parábola se abre hacia arriba, el vértice es el punto más bajo en el gráfico - llamado el mínimo, o min. Cuando la parábola se abre hacia abajo, el vértice es el punto más alto en el gráfico - llamado el máximo, o max.
Sólo parábolas verticales pueden tener valores mínimos o máximos, debido parábolas horizontales no tienen límite de qué tan alto o lo bajo que pueden ir. Encontrar el máximo de una parábola puede indicarle la altura máxima de una pelota lanzada al aire, la superficie máxima de un rectángulo, el valor mínimo de las ganancias de una empresa, y así sucesivamente.
Por ejemplo, digamos que un problema le pide que encontrar dos números cuya suma es 10 y cuyo producto es un máximo. Puede identificar dos ecuaciones diferentes escondidos en esta frase:
X + y = 10
xy = MAX
Si usted es como la mayoría de la gente, que no le gusta mezclar variables cuando usted no tiene que hacerlo, por lo que debe resolver una ecuación para una variable para sustituir a la otra. Este proceso es más fácil si a resolver la ecuación que no incluya min o max en absoluto. Así que si X + y = 10, se puede decir y = 10 - X. Puede conectar este valor en la otra ecuación para obtener lo siguiente:
(10 - X)X = MAX
Si distribuye el X en el exterior, se obtiene 10X - X2 = MAX. Este resultado es una ecuación de segundo grado para el que necesita para encontrar el vértice completando el cuadrado (que pone la ecuación en la forma que estamos acostumbrados a ver que identifica el vértice). Encontrar el vértice completando el cuadrado le da el valor máximo. Para ello, siga estos pasos:
Reorganizar los términos en orden descendente.
Este paso le da -X2 + 10X = MAX.
Factorizar el término principal.
Ahora tiene -1 (X2 - 10X) = MAX.
Completar el cuadrado.
Este paso se expande la ecuación a -1 (X2 - 10X + 25) = MAX - 25. Tenga en cuenta que -1 frente a los paréntesis convirtió el 25 en -25, que es por eso que debe agregar -25 a la derecha también.
Factor de la información dentro de los paréntesis.
Esto le da -1 (X - 5)2 = MAX - 25.
Mueva el constante al otro lado de la ecuación.
Se termina con -1 (X - 5)2 + 25 = MAX.
El vértice de la parábola es (5, 25). Por lo tanto, el número que usted está buscando (X) Es 5, y el producto máximo es de 25. Puede conectar 5 por X Llegar y en cualquiera de las ecuaciones: 5 + y = 10, o y = 5.
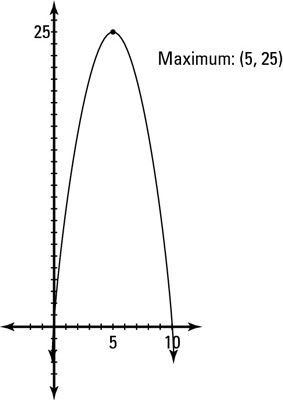
Esta figura muestra la gráfica de la función máxima para ilustrar que el vértice, en este caso, es el punto máximo.
-
¿Cómo encontrar los puntos máximos y mínimos en un gráfico -
Aplicando cuadráticas a situaciones de la vida real -
Curvas Crossing: encontrar las intersecciones de parábolas y círculos -
Encontrar las intersecciones de las líneas y las parábolas -
Cómo graficar parábolas - Completando el cuadrado para las secciones cónicas
Completando el cuadrado para pre-cálculo Ecuaciones cuadráticas se escriben en muchos formatos diferentes, dependiendo de lo que la aplicación actual. Completando el cuadrado es útil cuando estás escribiendo las cónicas en su forma estándar, y se puede utilizar este método para…
Las secciones cónicas en pre-cálculo Las secciones cónicas puede ser descrito o ilustrado con exactamente lo que su nombre indica: conos. Imagina un cono anaranjado en la calle, que dirigir en la dirección correcta. Entonces imaginar algún ingeniero de caminos inteligente colocar un…
Gráficas y funciones de transformación Puede graficar funciones bastante cómodamente utilizando una calculadora gráfica, pero se le frustró el uso de esta tecnología, si usted no tiene una buena idea de lo que vas a encontrar y donde usted lo encontrará. Usted necesita tener una…
Cómo completar el cuadrado Completando la plaza es muy útil cuando se le pide que resolver una ecuación cuadrática unfactorable y cuando es necesario para representar gráficamente las secciones cónicas (círculos, elipses, parábolas e hipérbolas).Sólo debe encontrar…
¿Cómo encontrar extremos absolutos sobre todo el dominio de una función Una función de absoluta max y absoluta min sobre su todo el dominio son los valores más altos y más bajos (alturas) de la función de cualquier lugar que está definido. Cuando se tiene en cuenta todo el dominio de una función, una función…
Cómo representar gráficamente una parábola horizontal Una parábola horizontal cuenta con sus propias ecuaciones para encontrar su partes- estos son sólo un poco diferente en comparación con una parábola vertical. La distancia al foco y la directriz desde el vértice en este caso es horizontal,…
Cómo representar gráficamente una parábola vertical, Con el fin de representar gráficamente una parábola correctamente, es importante tener en cuenta si es una horizontal o una parábola vertical. Esto es porque mientras que las variables y constantes en las ecuaciones para las dos curvas tienen el…
Cómo graficar funciones parentales En matemáticas, se ve ciertos gráficos una y otra vez. Por esa razón, estas, funciones comunes originales se llaman gráficos de los padres, e incluyen gráficas de funciones cuadráticas, raíces cuadradas, valores absolutos, cúbicas y raíces…
Cómo identificar las cuatro secciones cónicas en forma de ecuación Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…
¿Cómo resolver sistemas no lineales En un sistema no lineal, al menos una ecuación tiene una gráfica que no es una línea recta - es decir, al menos una de las ecuaciones tiene que ser no lineal. Su instructor de pre-cálculo le dirá que siempre se puede escribir una ecuación…
Truco Ley para cuadráticas: cómo encontrar rápidamente la ubicación del vértice de una parábola Para ahorrar tiempo al graficar una función cuadrática en la prueba ACT de matemáticas, puede encontrar rápidamente la ubicación del vértice de la parábola en relación con el y-eje. Sólo tienes que utilizar el siguiente truco sencillo…
Truco Ley para cuadráticas: cómo encontrar rápidamente la dirección de una parábola Para ahorrar tiempo al graficar una función cuadrática en la prueba ACT de matemáticas, puede determinar rápidamente la dirección de la parábola usando un simple truco basado en el coeficiente la.Este truco se relaciona con el signo de la…