Cómo representar gráficamente una parábola horizontal
Una parábola horizontal cuenta con sus propias ecuaciones para encontrar su partes- estos son sólo un poco diferente en comparación con una parábola vertical. La distancia al foco y la directriz desde el vértice en este caso es horizontal, porque se mueven a lo largo del eje de simetría, que es una línea horizontal. Por lo tanto, 1 / (4la
Conteúdo
El eje de simetría está en y = v, y el vértice se encuentra todavía en (h, v).
La atención se centra directamente a la izquierda oa la derecha del vértice, en el punto (h + 1.4la),v)
La directriz es la misma distancia desde el vértice como el foco en la dirección opuesta, por lo X = h - 1.4la.
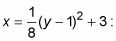  Agrandar1 Trabajar con la ecuación para encontrar el eje de simetría, distancia focal, y la directriz.Para encontrar el eje de simetría se inicia con el vértice. El vértice de esta parábola es (3, 1). El eje de simetría está en y = v, Así que para este ejemplo, es por lo y = 1. Para la ecuación dada, la = 1/8, y así la distancia focal es 2. Agregar este valor a h para encontrar el foco: (3 + 2, 1) o (5, 1). Para encontrar la directriz, restar la distancia focal de la Etapa 2 del h para encontrar la ecuación de la directriz. Debido a que esta es una parábola horizontal y el eje de simetría es horizontal, la directriz será vertical. La ecuación de la directriz es X = 3 - 2 o X = 1. | 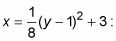Agrandar 2 Representa gráficamente la parábola y etiquetar sus partes.La figura que muestra el gráfico y tiene todas las piezas trazadas para usted. El foco se encuentra dentro de la parábola, y la directriz es una línea vertical 2 unidades desde el vértice. | 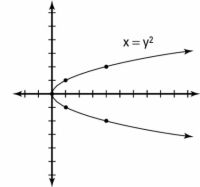 Agrandar3 Cuadrar las variables en la ecuación.La cuadratura de las variables en la ecuación de la parábola determina dónde se abre: Cuando y se eleva al cuadrado y X no lo es, el eje de simetría es horizontal y la parábola se abre izquierda o derecha. Por ejemplo, X = y2 es un parabola- horizontal se muestra en la figura. Sea consciente de coeficientes negativos en parábolas. Si la parábola es horizontal, un coeficiente negativo hará que la parábola abierta hacia la izquierda. |
Gráficas y funciones de transformación Puede graficar funciones bastante cómodamente utilizando una calculadora gráfica, pero se le frustró el uso de esta tecnología, si usted no tiene una buena idea de lo que vas a encontrar y donde usted lo encontrará. Usted necesita tener una…
¿Cómo encontrar una línea normal a una curva Una línea normal a una curva en un punto dado es la línea perpendicular a la línea que es tangente en ese mismo punto. Encontrar los puntos de perpendicularidad para todas las líneas normales a la parábolaque pasan por el punto (3,…
¿Cómo encontrar las líneas tangentes de una parábola que pasan por un punto determinado ¿Alguna vez quiso determinar la ubicación de una línea a través de un punto dado que es tangente a una curva dada? Por supuesto que tienes! He aquí cómo lo haces.Determinar los puntos de tangencia de las líneas por el punto (1, -1) que son…
Cálculo: cómo representar gráficamente una elipse Una elipse es básicamente un círculo que ha sido aplastado, ya sea horizontal o verticalmente. Desde una perspectiva de pre-cálculo, un elipse es un conjunto de puntos en un plano, la creación de un óvalo, forma curvada de tal manera que la…
Cómo representar gráficamente una parábola vertical, Con el fin de representar gráficamente una parábola correctamente, es importante tener en cuenta si es una horizontal o una parábola vertical. Esto es porque mientras que las variables y constantes en las ecuaciones para las dos curvas tienen el…
Cómo graficar una elipse Un elipse es un conjunto de puntos en un plano, la creación de un óvalo, forma curvada, de tal manera que la suma de las distancias desde cualquier punto de la curva a dos puntos fijos (la focos) Es una constante (siempre la misma). Una elipse es…
Cómo graficar funciones parentales En matemáticas, se ve ciertos gráficos una y otra vez. Por esa razón, estas, funciones comunes originales se llaman gráficos de los padres, e incluyen gráficas de funciones cuadráticas, raíces cuadradas, valores absolutos, cúbicas y raíces…
Cómo identificar las cuatro secciones cónicas en forma de ecuación Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…
Cómo identificar el mínimo y máximo en parábolas verticales Parábolas verticales dan una pieza importante de información: Cuando la parábola se abre hacia arriba, el vértice es el punto más bajo en el gráfico - llamado el mínimo, o min. Cuando la parábola se abre hacia abajo, el vértice es el punto…
Cómo identificar las cuatro secciones cónicas en forma de gráfico Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…
Truco Ley para cuadráticas: cómo encontrar rápidamente la ubicación del vértice de una parábola Para ahorrar tiempo al graficar una función cuadrática en la prueba ACT de matemáticas, puede encontrar rápidamente la ubicación del vértice de la parábola en relación con el y-eje. Sólo tienes que utilizar el siguiente truco sencillo…
Truco Ley para cuadráticas: cómo encontrar rápidamente la dirección de una parábola Para ahorrar tiempo al graficar una función cuadrática en la prueba ACT de matemáticas, puede determinar rápidamente la dirección de la parábola usando un simple truco basado en el coeficiente la.Este truco se relaciona con el signo de la…