Cómo graficar funciones parentales
En matemáticas, se ve ciertos gráficos una y otra vez. Por esa razón, estas, funciones comunes originales se llaman gráficos de los padres,
Conteúdo
Representación gráfica de funciones cuadráticas
Funciones cuadráticas son funciones en la que el segundo poder, o cuadrado, es la más alta a la que la cantidad o variable desconocida se eleva .. La función y= x2 o F(X) = X2 es una función cuadrática, y es el gráfico principal para todas las demás funciones cuadráticas.
El acceso directo a la gráfica de la función F(X) = X2 es comenzar en el punto (0, 0) (el origen) Y marcar el punto, llamado el vértice. Tenga en cuenta que el punto (0, 0) es el vértice de la función madre solamente. En cálculo, este punto se denomina punto crítico, y algunos maestros de pre-cálculo también usan esa terminología. Sin entrar en la definición de cálculo, significa que el punto es especial.
La gráfica de cualquier función cuadrática se llama parábola. Todas las parábolas tienen la misma forma básica. Para obtener los otros puntos, se trazan los puntos (1,12) = (1,1), (2,22) = (2,4), (3,32) = (3,9), etc. Esta gráfica se produce en el otro lado del vértice, así y sigue adelante, pero por lo general sólo un par de puntos a cada lado del vértice le da una buena idea de lo que la gráfica se parece.
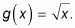
Esta figura muestra un ejemplo de una función cuadrática en forma de gráfico.
Representación gráfica de funciones de raíz cuadrada
LA gráfico de raíz cuadrada está relacionado con un gráfico cuadrática. El gráfico es cuadrática F(X) = X2, mientras que la gráfica de raíz cuadrada es g(X) = X2.1. La gráfica de una función de raíz cuadrada se parece a la mitad izquierda de una parábola que se ha girado 90 grados en sentido horario. También puede escribir la función de raíz cuadrada como
Sin embargo, sólo la mitad de la parábola existe, por dos razones. En primer lugar, existe el gráfico principal sólo cuando X es cero o positivo (porque no se puede encontrar la raíz cuadrada de números negativos [y mantenerlos reales, de todos modos]). En segundo lugar, existe la parábola sólo cuando g(X) Es positivo, porque cuando se le pide que encuentre
se le está pidiendo para encontrar sólo el director o la raíz positiva de X..
Esta gráfica comienza en el origen (0, 0) y luego se traslada a (1, sqrt (1)) = (1,1), (2, sqrt (2)), (3, sqrt (3)), etc.
Esta figura,
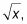
muestra la gráfica de la función raíz cuadrada de los padres
Observe que los valores que se obtienen mediante el trazado de puntos consecutivos no es exactamente lo que damos los números más bonitos. En su lugar, trate de valores por los que usted puede encontrar fácilmente la raíz cuadrada de picking. Así es como funciona esto: Comience en (0, sqrt (0)) = (0,0), y luego ir a (1, sqrt (1)) = (1,1), y luego a (4, sqrt (4)) = (4,2), y luego a (9, sqrt (9)) = (9,3), etc.
Representación gráfica de funciones de valor absoluto
La gráfica de los padres de valor absoluto de la función y = |X| convierte todos los no-negativo insumos (0 o positivo). Para representar gráficamente funciones de valor absoluto, se inicia en el origen y entonces cada número positivo se asigna la misma, mientras que cada número negativo se asigna a su contraparte positiva.
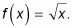
Esta figura muestra la gráfica de una función de valor absoluto.
Representación gráfica de funciones cúbicas
En un función cúbica, el grado más alto en cualquier variable es tres. La funcion F(X) = X3 es la función madre. Empiezas graficar el gráfico de la función de los padres cúbico en el origen (0, 0).
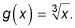
A partir de (0,0), realizar la representación gráfica (1,13) = (1,1), (2,23) = (2,8), etc., a la izquierda de (0,0) graficas (-1, (- 1)3) = (- 1, -1), (-2, (- 2)3) = (- 2, -8), etc .. La función madre cúbico, g(X) = X3, se muestra en forma de gráfico en esta figura.
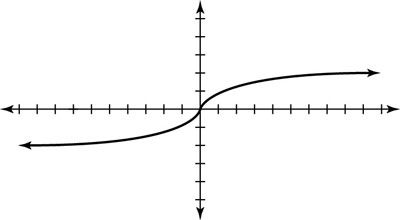
Representación gráfica de funciones de cubo de raíz
Funciones Cubo root están relacionados con funciones cúbicos de la misma manera que las funciones de raíz cuadrada están relacionados con funciones cuadráticas. Usted escribe funciones cúbicos como F(X) = X3 y funciones de cubo de raíz como g(X) = X03.01 o
Tomando nota de que una función de raíz cúbica es impar es importante porque ayuda a graficar ella.
Cómo ajustar el dominio y el rango de funciones combinadas Cuando comience la combinación de funciones (como la adición de un polinomio y una raíz cuadrada, por ejemplo), el dominio de la nueva función combinada se ve afectada. Lo mismo puede decirse de la gama de un combinado funcionalidad la nueva…
Cómo graficar y transformar una función exponencial Representación gráfica de una función exponencial es útil cuando se desea analizar visualmente la función. Si lo hace, le permite ver realmente el crecimiento o la decadencia de lo que estás tratando. La función madre básica de cualquier…
Cómo graficar funciones con más de una regla: funciones a nivel de pieza Funciones con más de una regla (llamados pfunciones IECE-sabios) Se rompen en pedazos, dependiendo de la entrada. Aunque una función a nivel de pieza tiene más de una función, cada función está definida sólo en un intervalo específico.…
Cómo graficar funciones parentales y troncos transformados Quieres un poco de buenas noticias, de forma gratuita? Representación gráfica de funciones de los padres y los registros transformadas es muy fácil! Usted puede cambiar cualquier registro en una expresión exponencial, por lo que este paso es lo…
Cómo graficar polinomios Aunque puede parecer desalentador, graficar polinomios es un proceso bastante sencillo. Una vez que haya encontrado los ceros de un polinomio, puede seguir unos sencillos pasos para representarla gráficamente.Por ejemplo, si ha encontrado los ceros…
Cómo graficar polinomios cuando las raíces son números imaginarios - una visión general En pre-cálculo y en el cálculo, ciertas funciones polinómicas tener raíces no reales además de raíces reales (y algunas de las funciones más complicadas tener todas raíces imaginarias). Cuando usted debe encontrar tanto, empezar por la…
Cómo identificar pares y funciones impares y sus gráficas Saber si una función es par o impar ayuda a graficar porque esa información le indica que la mitad de los puntos que usted tiene para graficar. Estos tipos de funciones son simétricas, por lo que lo que está en un lado es exactamente el mismo…
¿Cómo traducir el gráfico de una función Al mover un gráfico horizontal o verticalmente, esto se llama un traducción. En otras palabras, cada punto de la gráfica de los padres se traduce a la izquierda, derecha, arriba o abajo. La traducción siempre implica ningún tipo de adición o…
¿Cómo transformar verticalmente gráficos padres Cuando se aplica un vertical transformación a un gráfico padre, usted está estirando o encogiendo el gráfico a lo largo del y-eje, que cambia su altura. Un número (o coeficiente) Multiplicando en frente de una función provoca la…
Encuentre la imagen especular de una función de la trigonometría en un gráfico Cuando multiplicas una función trigonométrica de un número negativo, todos los valores de salida se invierten en la señal. Los valores positivos se vuelven negativos y los valores negativos se convierten en positivos. El efecto que esta…
Funciones Gráfico tangentes con multiplicadores variables En trigonometría, multiplicando el ángulo variable en una función tangente tiene el mismo efecto como lo hace con funciones seno y coseno - que afecta el periodo de la función. Si el múltiplo es 2, como en y = Tan 2X, a continuación, la…
Shift una función cosecante en un gráfico La función cosecante se ve afectada por los mismos principios de la multiplicación, suma, resta y que afectan a las otras funciones. Por ejemplo, añadiendo o restando un número hacia o desde los resultados de la función cosecante en el gráfico…