Gráficas y funciones de transformación

Puede graficar funciones bastante cómodamente utilizando una calculadora gráfica, pero se le frustró el uso de esta tecnología, si usted no tiene una buena idea de lo que vas a encontrar y donde usted lo encontrará. Usted necesita tener una idea bastante buena de lo alto o lo bajo y lo lejos a la izquierda y la derecha del gráfico se extiende.

Usted obtener información sobre estos aspectos de una gráfica de las intersecciones (donde la curva cruza los ejes), desde cualquier asíntotas (en funciones racionales), y, por supuesto, desde el dominio y el rango de la función. Un buen conocimiento de las características de los diferentes tipos de funciones va un largo camino para hacer que su experiencia de gráficos sea un éxito.

Otra forma de graficar funciones es reconocer las transformaciones realizadas en las definiciones de funciones básicas. Simplemente deslizando un gráfico a la izquierda oa la derecha o mover de un tirón el gráfico sobre una línea es mucho más fácil que empezar desde cero.

Usted va a trabajar con gráficos de la función de las siguientes maneras:

• Graficando tanto una función y su inversa

• La determinación de los vértices de las funciones cuadráticas (parábolas)

• Reconociendo los límites de algunas funciones radicales cuando graficar

• Señalando el punto de un gráfico de la función de valor absoluto superior o inferior para establecer su rango

• Resolución de ecuaciones polinómicas para intercepta

• Escribiendo ecuaciones de las asíntotas de funciones racionales

• El uso de transformaciones de función para graficar de forma rápida las variaciones en las funciones

Al graficar funciones, sus retos son los siguientes:

• Aprovechando formatos alternativos de ecuaciones de función (la forma pendiente-intersección, factorizado funciones polinómicas o racionales, y así sucesivamente)

• La determinación de si una parábola abre hacia arriba o hacia abajo y cómo abruptamente

• Representación gráfica de funciones radicales con raíces impares y reconociendo el dominio ilimitado

• Reconociendo cuando funciones polinómicas no cruzan la X-eje en un intercepto

• Usando asíntotas correctamente como una guía en la gráfica

• Reflejando funciones vertical u horizontalmente, dependiendo de la función de transformación

Problemas de práctica

1. Dada la gráfica de una función cuadrática, escribir su ecuación de la función en forma de vértice, y = la(X - h)² + k.

   

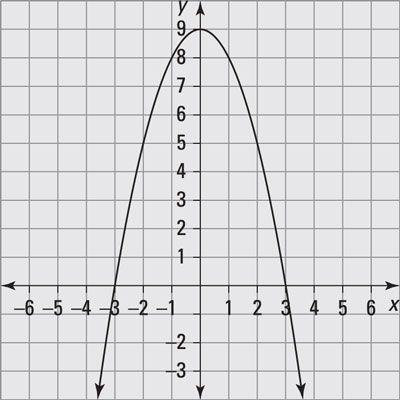
   Responder: y = -X² + 9

   El vértice es (0, 9), y el gráfico se abre hacia abajo. El uso de la forma vértice de una ecuación de segundo grado, y = la(X - h)² + k, estas características están representados por y = la(X - 0)² + 9, donde la es un número negativo.

   los X-intercepta son (# 8210-3, 0) y (3, 0). Suplente (3, 0) en la ecuación y resuelve para la:

   

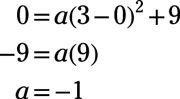
   Así que la ecuación de la parábola es y = -1 (X - 0)² + 9.

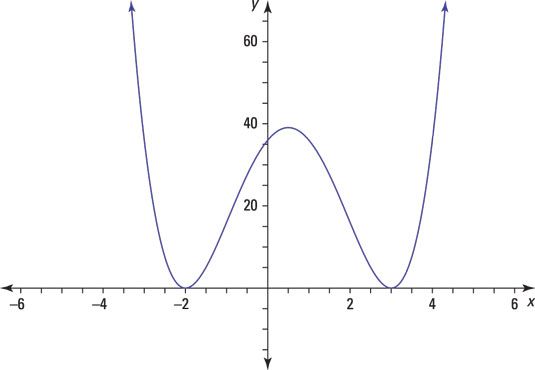
2. Determinar las intersecciones de la gráfica del polinomio. Luego trace la gráfica.

   F(X) = (X - 3)²(X + 2)²

   Responder: intercepta: (3,0), (# 8210-2,0), (0, 36)

   Encuentra el X-intercepta por dejar y = 0 y despejando X. los X-intercepciones de y = (X - 3)²(X + 2)² son (3, 0) y (# 8210-2, 0).

   Encuentra el y-intercepción dejando X = 0 y despejando y. los y-intersección es (0, 36).

   Para trazar la gráfica, tenga en cuenta que los exponentes de los factores son números pares, por lo que la curva apenas toque la X-eje en cada X-intercepción. La curva se eleva hacia la derecha como X tiende a infinito positivo, tal como se determina cuando se prueba una X valor superior a la derecha, la mayoría de intercepción. Aquí está el gráfico: