Cómo graficar una función racional con numerador y el denominador de la igualdad de grados

categoría Educación y lenguas / Matemáticas / Cálculo

Después de calcular todas las asíntotas y la X- y y-intercepciones para una función racional, que tienen toda la información que necesita para empezar a graficar la función. Funciones racionales con igualdad de grados en el numerador y el denominador se comportan de la manera que lo hacen debido a los límites. Lo que hay que recordar es que la asíntota horizontal es el cociente de los principales coeficientes de la parte superior y la parte inferior de la función.

Echa un vistazo a

image0.jpg

que tiene la igualdad de grados en las variables para cada parte de la fracción. Siga estos sencillos pasos para graficar g(X), Que se muestra en esta figura:

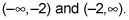
image1.jpg

  1. Dibuje la asíntota vertical (s) de g(X).

    Representación gráfica de la asíntota vertical primero muestra el número en el dominio donde el gráfico no puede pasar a través. La gráfica se acerca a este punto, pero nunca llega a él. Con esto en mente, ¿qué valor (s) de X puedes no conectar a la función racional?

  1. Ajuste el denominador de la función racional igual a cero.

    por g(X), 4 -3X = 0.

  2. Resuelva esta ecuación para X.

    4 - 3X = 0

    X = 4/3

Usted encontrará sólo una asíntota vertical en X = 3.4, lo que significa que tiene sólo dos intervalos a considerar:

image2.jpg

  • Dibuje la asíntota horizontal para g(X).

    Para encontrar una asíntota horizontal de una función racional, que hay que buscar en el grado de los polinomios en el numerador y el denominador. los grado es la mayor potencia de la variable en la expresión polinómica.

    La funcion g(X) Tiene iguales grados en la parte superior e inferior. Para encontrar la asíntota horizontal, divida los principales coeficientes de los términos de más alto grado:

    image3.jpg

    Ahora tiene su asíntota horizontal para g(X). Así que ahora puede dibujar una línea horizontal en esa posición.

  • Trazar la X- y y-intercepta para g(X).

    La pieza final del rompecabezas es encontrar las intersecciones (donde la línea o curva cruza la X- y y-ejes) de la función racional, si existe alguno:

    • Para encontrar la y-intersección de una ecuación, ajuste X = 0. (Enchufe 0 donde vea X.) Los y-intersección de g(X), Por ejemplo, es:

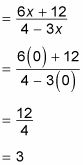
      image4.jpg

      Entonces el y-intersección de g(X) Es 3.

    • Para encontrar la X-intersección de una ecuación, ajuste y = 0 y resolver para X:

      Para cualquier función racional, el acceso directo a la búsqueda de la X-intercepción es establecer el numerador igual a cero y luego resolver. A veces, cuando lo hace, sin embargo, la ecuación que se obtiene es irresoluble, lo que significa que la función racional no tiene un X-intercepción.

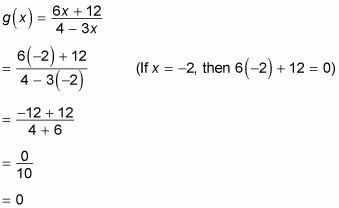
      image5.jpg

      Por lo tanto, g(X) Tiene una X-interceptar a -2.

    • Utilice los valores de prueba de su elección para determinar si el gráfico está por encima o por debajo de la asíntota horizontal.

      Los dos intercepciones ya se encuentran en el primer intervalo y por encima de la asíntota horizontal, por lo que saben que el gráfico en todo ese intervalo está por encima de la asíntota horizontal (se puede ver fácilmente que g(X) Puede nunca es igual a -2). Ahora, elija un valor de prueba para el segundo intervalo mayor que 4/3. Por ejemplo, si usted elige X = 2, entonces Sustituyendo esto en la función g(X) Le otorga -12. Usted sabe que el -12 es manera bajo -2, para que sepa que la vida del gráfico bajo la asíntota horizontal en este segundo intervalo.



      • Artículos Relacionados

      Sobre el autor
      ¿Cómo distinguir expresiones racionales propias e impropias ¿Cómo distinguir expresiones racionales propias e impropias

      Integración por fracciones parciales sólo funciona con expresiones racionales adecuadas, pero no con expresiones racionales impropias. Decirle a una fracción propia a partir de uno inadecuada es fácil: Una fracción a / b es correcta si el…

      Cómo evaluar una integral impropia que es verticalmente infinita Cómo evaluar una integral impropia que es verticalmente infinita

      Integrales impropias son útiles para resolver una variedad de problemas. LA verticalmente infinita integral impropia contiene al menos una asíntota vertical. Verticalmente integrales impropias infinitos son más difíciles de reconocer que los que…

      ¿Cómo encontrar extremos absolutos sobre todo el dominio de una función ¿Cómo encontrar extremos absolutos sobre todo el dominio de una función

      Una función de absoluta max y absoluta min sobre su todo el dominio son los valores más altos y más bajos (alturas) de la función de cualquier lugar que está definido. Cuando se tiene en cuenta todo el dominio de una función, una función…

      ¿Cómo encontrar la ecuación de asíntotas ¿Cómo encontrar la ecuación de asíntotas

      En pre-cálculo, puede que tenga que encontrar la ecuación de asíntotas para ayudarle a esbozar las curvas de una hipérbola. Debido a hipérbolas están formados por una curva donde la diferencia de las distancias entre dos puntos es constante,…

      Cómo graficar una función cosecante Cómo graficar una función cosecante

      Cosecante es casi exactamente el mismo que el secante porque es el recíproco de sine (a diferencia de coseno). En cualquier lugar de seno tiene un valor de 0, se ve una asíntota en el gráfico cosecante. Debido a la gráfica cruza el sine X-eje…

      Cómo graficar y transformar una función exponencial Cómo graficar y transformar una función exponencial

      Representación gráfica de una función exponencial es útil cuando se desea analizar visualmente la función. Si lo hace, le permite ver realmente el crecimiento o la decadencia de lo que estás tratando. La función madre básica de cualquier…

      Cómo graficar una función racional cuando el numerador tiene el grado más alto Cómo graficar una función racional cuando el numerador tiene el grado más alto

      Funciones racionales donde el numerador tiene el mayor grado en realidad no tienen asíntotas horizontales. En cambio, tienen asíntotas oblicuas que se encuentra utilizando la división larga.Por ejemplo, el gráfico h (X):Dibuje la asíntota…

      Cómo graficar una función racional con denominador que tiene el grado más alto Cómo graficar una función racional con denominador que tiene el grado más alto

      Después de calcular todas las asíntotas y la X- y y-intercepciones para una función racional, que tienen toda la información que necesita para empezar a graficar la función. En cualquier función racional donde el denominador tiene un grado…

      Cómo graficar una función racional con numerador tiene el grado más alto Cómo graficar una función racional con numerador tiene el grado más alto

      Después de calcular todas las asíntotas y la X- y y-intercepciones para una función racional, que tienen toda la información que necesita para empezar a graficar la función. Funciones racionales donde el numerador tiene el mayor grado en…

      Cómo graficar una función secante Cómo graficar una función secante

      Puede representar gráficamente una función secante F(X) = Sec X mediante el uso de medidas similares a las de tangente y cotangente. Al igual que con tangente y cotangente, la gráfica de la secante tiene asíntotas. Esto es porque secante se…

      Cómo graficar una función tangente Cómo graficar una función tangente

      La función tangente tiene una gráfica de los padres al igual que cualquier otra función. Utilizando la gráfica de esta función, se puede hacer el mismo tipo de transformación que se aplica a la gráfica de los padres de cualquier función. La…

      Cómo graficar funciones parentales y troncos transformados Cómo graficar funciones parentales y troncos transformados

      Quieres un poco de buenas noticias, de forma gratuita? Representación gráfica de funciones de los padres y los registros transformadas es muy fácil! Usted puede cambiar cualquier registro en una expresión exponencial, por lo que este paso es lo…

      » » » » Cómo graficar una función racional con numerador y el denominador de la igualdad de grados