¿Cómo encontrar extremos absolutos sobre todo el dominio de una función

Una función de absoluta max y absoluta min sobre su todo el dominio son los valores más altos y más bajos (alturas) de la función de cualquier lugar que está definido. Cuando se tiene en cuenta todo el dominio de una función, una función puede tener un máximo absoluto o min o ambos o ninguno. Por ejemplo, la parábola y = X² tiene un mínimo absoluto en el punto (0,0) - la parte inferior de su forma de copa - pero ningún máximo absoluto porque va para siempre a la izquierda y la derecha. Se podría pensar que su absoluta máximo sería infinito, pero el infinito no es un número y por lo tanto, no puede considerarse como un máximo (lo mismo para el uso infinito negativo como mínimo absoluto).

Por un lado, la idea del punto más alto de una función y punto más bajo parece bastante simple, ¿no? Pero hay una llave en las obras. La llave es la categoría de las cosas que don't calificar como Maxes o minutos.

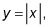
En la figura, hay "puntos finales" vacías como (3,4) en F (X). F (X) No tiene un máximo absoluto. Su máximo no es 4 porque nunca llega a 4, y su máximo no puede ser cualquier cosa menos de 4, como 3.999, porque se pone más alta que, digamos 3,9999. Del mismo modo, un agujero de infinitesimal en una función no se puede calificar como un max o min. Por ejemplo, considere la función valor absoluto,

usted sabe, la función en forma de V con la esquina aguda en el origen. No tiene máximo absoluto porque va hasta el infinito. Su absoluta min es cero (en (0, 0), por supuesto). Pero ahora, digamos que altera la función ligeramente por arrancarse el punto en (0, 0) y dejando un agujero infinitesimal allí. Ahora, la función no tiene mínimo absoluto.

Consideremos ahora g (X) En la figura. Se muestra otro tipo de situación que no califica como un mínimo (o máximo). g (X) No tiene min absoluta. Ir a la izquierda, g se arrastra a lo largo de la asíntota horizontal en y = 0, siempre cada vez menor, pero nunca conseguir un precio tan bajo como cero. Ya que nunca llega a cero, el cero no puede ser el mínimo absoluto, y no puede ser de otra min absoluta (como, por ejemplo, 0,0001), porque en cierto modo punto a la izquierda, g recibirá por debajo de cualquier pequeño número puede nombrar.

Teniendo esto en mente, aquí es un enfoque paso a paso para la localización de una función absoluta máxima y mínima (si las hay):

1. Encuentre la altura de la función en cada uno de sus números críticos. (Recordemos que los números críticos de una función son los X-valores dentro del dominio de la función donde el derivado es cero o indefinido.)

   Considerar todas los números críticos, no sólo aquellos en un intervalo dado. El mayor de estos valores será absoluto máximo de la función a menos que la función va más alto que el punto en el que caso de que la función no tendrá un máximo absoluto. El más bajo de estos valores será absoluta min de la función a menos que la función va más bajo que el punto en el que caso de que no tendrá un min absoluta. Los pasos 2 y 3 le ayudará a determinar si la función va más alto que el más alto punto crítico y / o más bajo que el punto crítico más bajo. Si se aplica el paso 1 para g (X) En la figura, usted encontrará que no tiene puntos críticos. Cuando esto sucede, ya está hecho. La función no tiene ni un máximo absoluto, ni un mínimo absoluto.

2. Compruebe si la función va hasta el infinito y / o hacia abajo hasta el infinito negativo.

   Si una función sube infinito positivo o hacia abajo hasta el infinito negativo, lo hace a su extrema derecha o hacia la izquierda o en una asíntota vertical. Por lo tanto, evaluar

   

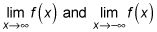
   - la llamada comportamiento final de la función - y el límite de la función como X enfoques cada asíntota vertical (si los hay) de la izquierda y desde la derecha. Si la función sube hasta el infinito, no tiene max- absoluta si se cae al infinito negativo, no tiene min absoluta.

3. Grafica la función para comprobar si hay asíntotas horizontales y características extrañas como la discontinuidad de salto en F (X) En la figura.

   Mira la gráfica de la función. Si usted ve que la función se hace mayor que el más alto de sus puntos críticos, no tiene max- absoluta si se va más bajo que el más bajo de sus puntos críticos, no tiene min absoluta. La aplicación de este proceso de 3 pasos para F (X) En la figura, Paso 1 revelaría dos puntos críticos: el punto final al (3, 1) y el máximo local en más o menos (4.1, 1.3). En el paso 2, se verá que F desciende hasta el infinito negativo y por lo tanto no tiene min absoluta. Finalmente, en el paso 3, verías que F va más alto que el más alto de los puntos críticos, (4.1, 1.3), y que, por lo tanto, no tiene máximo absoluto. ¡Ya terminaste!