¿Cómo encontrar los números críticos de una función
Todos los extremos locales se producen en los puntos críticos de una función - que es donde la derivada es cero o indefinido (pero no se olvide que los puntos críticos no siempre son extremos locales). Así, el primer paso en la búsqueda de extremos locales de una función es encontrar los números críticos (el X-valores de los puntos críticos).
He aquí un ejemplo: Encontrar los números críticos de F (X) = 3X5 - 20X3, como se muestra en la figura.
Esto es lo que hace:
Encuentra la primera derivada de F usando la regla de la potencia.
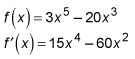
Establezca la igualdad derivada a cero y resolver para X.
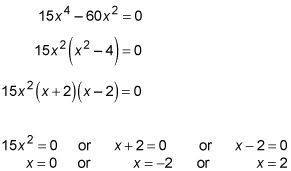
Estas tres X-los valores son números críticos de F. Números críticos adicionales podrían existir si la primera derivada se indefinido en algún X-valores, pero debido a que el derivado, 15X4- 60X2, está definida para todos los valores de entrada, el conjunto solución anterior, 0, -2 y 2, es la lista completa de los números críticos. Debido a que el derivado de F es igual a cero en estos tres números críticos, la curva tiene tangentes horizontales en estos números. En la figura, se puede ver las pequeñas líneas tangentes horizontales dibujadas donde X = -2 Y X = 2. La tercera línea horizontal tangente en X = 0 es el X-eje.
Una curva tiene una tangente horizontal donde su derivada es cero, es decir, en sus puntos estacionarios. Una curva tendrá líneas tangentes horizontales en todos sus minutos y Maxes locales (a excepción de las esquinas agudas) y en todos sus puntos de inflexión horizontales.
Ahora que tienes la lista de los números críticos, es necesario determinar si los picos o valles o puntos de inflexión se producen en los X-los valores. Usted puede hacer esto, ya sea con la primera prueba derivado o la segunda derivada. Usted se estará preguntando por qué tienes que probar los números críticos cuando se puede ver en los picos y los valles son con sólo mirar el gráfico de la figura - que se puede, por supuesto, reproducir en tu calculadora gráfica. Buen punto. Bien, así que este problema - sin mencionar un sinnúmero de otros problemas que has hecho en los cursos de matemáticas - es algo artificial y poco práctico. Entonces, ¿qué más hay de nuevo?
-
Encuentra la pendiente de una curva con la TI-84 Plus -
Grafica la derivada de una función en la TI-84 Plus -
Comando Derivada de TI-Nspire submenú cálculo cas -
Cómo gráficas de derivados difieren de gráficas de funciones -
Cómo analizar la posición, velocidad y aceleración con la diferenciación -
¿Cómo encontrar extremos absolutos sobre todo el dominio de una función
¿Cómo encontrar extremos absolutos en un intervalo cerrado Cada función que es continua en un intervalo cerrado tiene un valor máximo absoluto y un valor mínimo absoluto (el extremos absolutos) en ese intervalo - en otras palabras, un punto más alto y más bajo - aunque puede haber un empate en el valor…
¿Cómo encontrar derivados de alto orden Encontrar un segundo, tercero, cuarto, o superior derivado es increíblemente simple. La segunda derivada de una función es simplemente la derivada de su primera derivada. La tercera derivada es la derivada de la segunda derivada, el cuarto…
¿Cómo encontrar extremos locales con la primera prueba derivada Todos los máximos y mínimos locales en el gráfico de una función - llamada extremos locales - se producen en los puntos críticos de la función (donde la derivada es cero o no definido). (No hay que olvidar, sin embargo, que no todos los puntos…
¿Cómo encontrar la derivada de una línea los derivado es sólo un término de cálculo de lujo para una idea simple que usted probablemente sabe de álgebra - pendiente. Slope es el término álgebra de lujo para la inclinación. Y lo escarpado es la palabra elegante para. . . ¡No! La…
¿Cómo encontrar las líneas tangentes de una parábola que pasan por un punto determinado ¿Alguna vez quiso determinar la ubicación de una línea a través de un punto dado que es tangente a una curva dada? Por supuesto que tienes! He aquí cómo lo haces.Determinar los puntos de tangencia de las líneas por el punto (1, -1) que son…
¿Cómo saber cuando un derivado no existe Hay tres situaciones en las que un derivado de falla de existir. La derivada de una función en un punto dado es la pendiente de la recta tangente en ese punto. Por lo tanto, si no se puede trazar una línea tangente, no hay derivada - que sucede en…
Cómo localizar intervalos de puntos de inflexión y concavidad Puede localizar la concavidad de una función (donde una función es cóncava hacia arriba o hacia abajo) y los puntos de inflexión (donde los interruptores concavidad de positivo a negativo o vice versa) en unos sencillos pasos. El siguiente…
Cómo utilizar la diferenciación para calcular el volumen máximo de una caja Uno de los usos más prácticos de la diferenciación es encontrar el valor máximo o mínimo de una función en el mundo real. En el siguiente ejemplo, se calcula el volumen máximo de una caja que no tiene la parte superior y que es ser fabricado…
El teorema fundamental del cálculo El teorema fundamental del cálculo es uno de los teoremas más importantes en la historia de las matemáticas. Establece que, dada una función de área LAF que barre área bajo F (t),la velocidad a la que el área está siendo barrido es igual a…
Comprobación de confianza valores críticos de intervalos estadísticos Los valores críticos (z*-valores) son un componente importante de los intervalos de confianza (la técnica estadística para estimar parámetros poblacionales). los z*-valor, que aparece en el margen de la fórmula de error, mide el número de…
Encuentra los valores críticos de dos colas cuando se prueba una hipótesis para una muestra grande En estadística, una amplia muestra tiene un tamaño mayor o igual a 30. Cuando se utiliza una gran muestra para probar una hipótesis acerca de una media poblacional, el valor o valores críticos resultante de dos colas de la distribución normal…
En cuanto a los valores críticos del intervalo de confianza Los valores críticos (z*-valores) son un componente importante de los intervalos de confianza (la técnica estadística para estimar parámetros poblacionales). los z* -valor, que aparece en el margen de la fórmula de error, mide el número de…