Cómo gráficas de derivados difieren de gráficas de funciones

Cuando se empieza a observar las gráficas de los derivados, puede caducar fácilmente en pensar en ellos como funciones regulares - pero no lo son. Afortunadamente, usted puede aprender mucho acerca de las funciones y sus derivados mirando su lado a lado los gráficos y la comparación de sus características importantes. Por ejemplo, tomemos la función, F (X) = 3X⁵ - 20X³.

Ahora va a viajar a lo largo F de izquierda a derecha, haciendo una pausa para observar sus puntos de interés y también observar lo que está sucediendo a la gráfica de

en los mismos puntos. Pero en primer lugar, echa un vistazo a la siguiente (largo) de advertencia.

Esto no es la función! Como nos fijamos en la gráfica de

en la figura, o la gráfica de cualquier otro derivado, puede que tenga que dar una palmada a ti mismo en la cara cada minuto o así para recordar que "Este es el derivado Estoy mirando, no la función! "Es fácil confundir gráficas de derivados para las funciones regulares. Es posible que, por ejemplo, mirar a un intervalo que va para arriba en la gráfica de un derivado y por error concluir que la función original también debe estar pasando en el mismo intervalo - un error comprensible.

Usted sabe la primera derivada es lo mismo que cuesta. Así que cuando vea la gráfica de la primera derivada de subir, usted puede pensar, "Oh, la primera derivada (la pendiente) está subiendo, y cuando la pendiente sube eso es como subir una colina, por lo que la función original debe ser naciente ". Esto suena razonable, ya que, libremente hablando, usted puede describir la parte frontal de una colina como una pendiente que va hacia arriba, cada vez mayor. Pero matemáticamente hablando, el lado frontal de una colina tiene una positivo pendiente, no necesariamente un creciente cuesta abajo. Así, donde una función es creciente, la gráfica de su derivado será positivo, pero ese gráfico derivado podría ser ir hacia arriba o hacia abajo.

Digamos que usted está subiendo una colina. Al acercarse a la cima de la colina, usted todavía va arriba, pero, en general, la cuesta abajo (la pendiente) va abajo. Puede ser que sea 3, luego 2, luego 1 y, a continuación, en la parte superior de la colina, la pendiente es cero. Así que la pendiente se hace más pequeño o decreciente, incluso cuando usted está subiendo la colina o creciente. En un intervalo tal, el gráfico de la función es aumentando, pero la gráfica de su derivado es decreciente. ¿Lo tengo?

De acuerdo, vamos a volver a la F y su derivado en la figura. A partir de la izquierda y viajar hacia la derecha, F aumenta hasta que el máximo local en (-2, 64). Va hacia arriba, por lo que su pendiente es positivo, pero F está recibiendo cada vez menos empinadas, así que su pendiente es decreciente - la pendiente disminuye hasta que se hace cero en el pico. Esto corresponde a la gráfica de

(la pendiente), que es positivo (porque es por encima de la X-eje), pero decreciente a medida que avanza hasta el punto (2, 0). Vamos a resumir todo su viaje a lo largo de F y

con la siguiente lista de reglas.

• Un creciente en un intervalo de función corresponde a un intervalo en el gráfico de su derivado que es positivo (o cero para un solo punto si la función tiene un punto de inflexión horizontal). En otras palabras, el aumento de intervalo de una función corresponde a una parte de la gráfica derivado que está por encima de la X-eje (o que toca el eje para un único punto en el caso de un punto de inflexión horizontal). Ver intervalos A y F en la figura.

• Un local max en el gráfico de una función (como (-2, 64) corresponde a una cero (un X-intercepción) en un intervalo de la gráfica de su derivado que atraviesa la X-eje ir abajo (como en (2, 0)).

En un gráfico derivado, que'he conseguido un m-eje. Cuando usted está buscando en varios puntos de la gráfica derivado, no se olvide de que el y-de coordenadas de un punto, como (2, 0), en un gráfico de un derivado que la primera dice cuesta abajo de la función original, no su altura. Piense en el y-eje sobre el primer gráfico derivado como la cuesta abajo-eje o la m-eje- usted podría pensar en puntos generales sobre el primer gráfico derivado de tener coordenadas (X, m).

• LA decreciente intervalo en una función corresponde a una negativo intervalo en el gráfico de la derivada (o cero para un solo punto si la función tiene un punto de inflexión horizontal). El intervalo negativo en el gráfico derivado es por debajo de la X-eje (o en el caso de un punto de inflexión horizontal, el gráfico derivado toca el X-eje en un solo punto). Ver intervalos B, C, D y E en la figura (pero tenga en cuenta como una sola sección), en donde F se cae todo el camino desde el máximo local en (-2, 64) al mínimo local en (2, -64) y donde

  

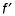
  es negativa entre (-2, 0) y (2, 0), excepto en el punto (0, 0) en

  

  que se corresponde con el punto de inflexión en horizontal F.

• Un local min en el gráfico de una función corresponde a un cero (una X-intercepción) en un intervalo de la gráfica de su derivado que atraviesa la X-eje que sube (como en (2, 0)).

Ahora vamos a echar un segundo viaje a lo largo F para considerar sus intervalos de concavidad y sus puntos de inflexión. En primer lugar, tenga en cuenta los intervalos de A y B en la figura. La gráfica de F es cóncava hacia abajo - que significa lo mismo que un decreciente pendiente - hasta que llega al punto de inflexión en alrededor (-1,4, 39,6).

Por lo tanto, la gráfica de

disminuye hasta que toque fondo en alrededor de (-1.4, -60). Estas coordenadas te dicen que el punto de inflexión en el -1,4 en F tiene una pendiente de -60. Tenga en cuenta que punto de la inflexión F al (-1,4, 39,6) es el punto de mayor pendiente en ese tramo de la función, pero tiene la más pequeño pendiente debido a su pendiente es una más grande negativo que la pendiente en cualquier otro punto cercano.

Entre (-1,4, 39,6) y el siguiente punto de inflexión en (0, 0), F es cóncava hacia arriba, lo que significa lo mismo que un creciente cuesta abajo. Así que la gráfica de

aumenta de alrededor de -1,4 a donde se realiza un máximo local en (0, 0). Ver intervalo de C en la figura. Vamos a tomar un descanso de este viaje por algunas más reglas.

• A cóncava abajo intervalo en el gráfico de una función corresponde a una decreciente intervalo en el gráfico de sus derivados (intervalos de A, B, y D en la figura). Y un cóncava arriba intervalo de la función corresponde a un creciente intervalo en el derivado (intervalos C, E, y F).

• Un punto de inflexión en una función (a excepción de un punto de inflexión vertical donde está definido el derivado) corresponde a una extremo local en el gráfico de su derivado. Un punto de inflexión mínimo pendiente (en su vecindad) corresponde a un local de min sobre el derivado ficos un punto de inflexión máximo pendiente (en su vecindad) corresponde a un local de max en el gráfico derivado.

Reanudación de su viaje, después de (0, 0), F es cóncava hacia abajo hasta el punto de inflexión en alrededor (-1,4, 39,6) - esto corresponde a la sección decreciente de

a partir de (0, 0) a su min a (1,4, -60) (D intervalo en la figura). Finalmente, F es cóncava hacia arriba el resto del camino, que corresponde a la sección creciente de

a partir de las (1,4, -60) (intervalos E y F en la figura).

Bueno, que prácticamente te lleva al final del camino. Volviendo adelante y hacia atrás entre las gráficas de una función y su derivado puede ser muy tratando al principio. Si tu cabeza comienza a girar, tomar un descanso y volver a estas cosas más tarde.

Ahora, mira de nuevo en la gráfica de la derivada,

en la figura y también en el gráfico de señal para

en la siguiente figura.

Ese gráfico muestra, porque es un segundo gráfico signo derivado, lleva exactamente (bueno, casi exactamente) la misma relación con la gráfica de

como un primer derivados osos gráfico signo a la gráfica de una función regular. En otras palabras, negativo intervalos en el gráfico de signo en la figura

le mostrará dónde la gráfica de

es decreciente- positivo intervalos en el gráfico signo

le mostrará dónde

es creciente. Y los puntos donde los signos cambian de positivo a negativo o vice versa

le mostrará dónde

tiene extremos locales.