¿Cómo diferenciar funciones inversas
Hay una fórmula difícil buscar la participación de las derivadas de las funciones inversas, pero antes de llegar a eso, a ver la figura siguiente, que resume muy bien la idea.
Esta cifra muestra un par de funciones inversas, F y g. Funciones inversas son simétricas con respecto a la línea, y = X. Como con cualquier par de funciones inversas, si el punto (10, 4) es de una sola función, (4, 10) está en su inversa. Y, debido a la simetría de las gráficas, se puede ver que las pistas de esos puntos son recíprocos:
Así es como la idea funciona gráficamente.
La explicación algebraica es un poco más complicado, sin embargo:
Escribir el punto (10, 4) en F como (10, F (10)).
Expresar la pendiente en este punto (que es el derivado) como
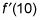
Escribir el punto (4, 10) en g como (4, g (4)).
Porque F (10) = 4, reemplace las 4s en (4, g (4)) con F (10) s.
Esto le da (F (10), g (F (10))).
Expresar la pendiente (el derivado) en este punto, como
Esta ecuación difícil mirar expresa nada más y nada menos que los dos triángulos en las dos funciones en la figura anterior.
En palabras, esta fórmula dice que la derivada de una función, f, con respecto a X, es el recíproco de la derivada de su inversa con respecto a f.
Cómo graficar funciones parentales y troncos transformados Quieres un poco de buenas noticias, de forma gratuita? Representación gráfica de funciones de los padres y los registros transformadas es muy fácil! Usted puede cambiar cualquier registro en una expresión exponencial, por lo que este paso es lo…
Cómo graficar la inversa de una función Si se le pregunta para representar gráficamente la inversa de una función, puede hacerlo recordando un hecho: una función y su inversa se reflejan sobre la línea y = X. Esta línea pasa por el origen y tiene una pendiente de 1.Cuando se le pide…
Cómo interpretar las gráficas de funciones Vas a ver a decenas y decenas de funciones en su estudio del cálculo, y las gráficas de estas funciones puede expresar visualmente las cosas tales como la inflación, el crecimiento demográfico y la desintegración radiactiva. A continuación se…
¿Cómo saber cuando un derivado no existe Hay tres situaciones en las que un derivado de falla de existir. La derivada de una función en un punto dado es la pendiente de la recta tangente en ese punto. Por lo tanto, si no se puede trazar una línea tangente, no hay derivada - que sucede en…
Cómo reconocer funciones inversas Se puede decir que dos funciones son funciones inversas cuando cada una deshace lo que el otro hace. Al graficar funciones inversas, cada uno es una imagen especular de la otra. Estos son algunos ejemplos de funciones inversas:Usted puede escribir…
Cómo para verificar la inversa de una función A veces, su libro de texto o maestro puede pedirle que verifique que dos funciones dadas son en realidad inversas entre sí. Para ello, es necesario demostrar que tanto F(g(X)) Y g(F(X)) = X.Cuando se le pide que encontrar una inversa de una…
Una tabla rápida para las tres funciones trigonométricas recíprocas Funciones recíprocas tienen valores que son recíprocos, o voltea, de los valores de sus respectivas funciones. El recíproco de seno es cosecant, por lo que cada valor de la función es la inversa de la correspondiente ángulo de sine de. Lo mismo…
Funciones Gráfico de seno y coseno inversa Las gráficas de las funciones trigonométricas inversas son relativamente singularidad por ejemplo, seno inverso y el coseno inversa son un poco brusca y desarticulada. Estos gráficos son importantes debido a su impacto visual. Especialmente en el…
Funciones Gráfico tangente inversa y cotangente Las gráficas de las funciones tangente y cotangente son muy interesantes porque implican dos asíntotas horizontales. Las asíntotas ayudan con las formas de las curvas y hacer hincapié en el hecho de que algunos ángulos no funcionarán con las…
Gráfico secante inversa y cosecante Las gráficas de las funciones cosecante secantes e inversas inversas tomarán un poco de explicación. En primer lugar, tener en cuenta que las funciones secante y cosecante no tienen valores de salida (y-valores) entre -1 y 1, por lo que un…
¿Cómo encontrar una función trigonométrica inversa Las funciones trigonométricas inversas todos tienen, pero sólo en condiciones especiales - usted tiene que restringir los valores de dominio. No todas las funciones tienen inversos, y no todos los inversos son fáciles de determinar. Aquí es un…
¿Cómo encontrar la inversa de una función trigonométrica Utilice las funciones trigonométricas inversas para resolver ecuaciones como pecado X = 1/2, sec X = -2, O moreno 2X = 1. En las ecuaciones típicas de álgebra, puede resolver por el valor de X dividiendo cada lado de la ecuación por el…