¿Cómo saber cuando un derivado no existe
Hay tres situaciones en las que un derivado de falla de existir. La derivada de una función en un punto dado es la pendiente de la recta tangente en ese punto. Por lo tanto, si no se puede trazar una línea tangente, no hay derivada - que sucede en los casos 1 y 2 a continuación. En el caso 3, hay una línea tangente, pero su pendiente y el derivado son indefinidos.
Las tres situaciones se muestran en la siguiente lista.
Cuando no hay línea tangente y por lo tanto no derivada en cualquiera de los tres tipos de discontinuidad:
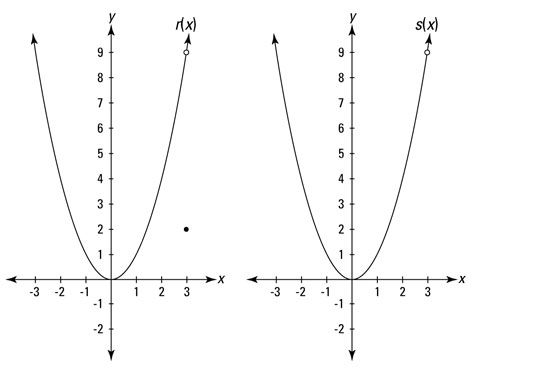
LA discontinuidad removible - eso es un término de lujo para un agujero - como los agujeros en funciones r y s en la figura anterior.
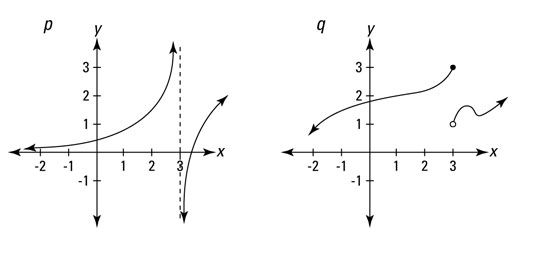
Un discontinuidad infinita como en X = 3 en la función p en la figura anterior.
LA saltar discontinuidad como en X = 3 en la función q en la figura anterior.
La continuidad es, por lo tanto, una necesario condición para la diferenciabilidad. No es, sin embargo, una suficiente condición de los próximos dos casos muestran. Cavar que lógico-hablar.
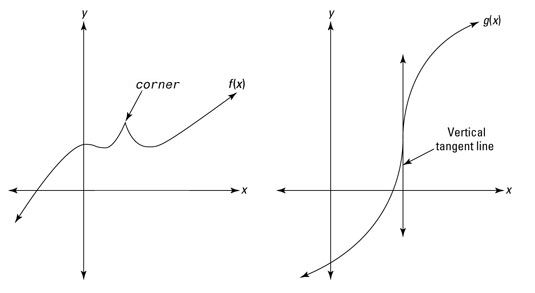
Cuando no hay línea tangente y por lo tanto no derivada en un fuerte esquina en una función. Ver la función F en la figura anterior.
Cuando una función tiene una punto de inflexión vertical,. En este caso, la pendiente no está definida y por lo tanto el derivado de no existir. Ver la función g en la figura anterior.
-
Encuentra la pendiente de una curva en la TI-83 Plus -
Encuentra la pendiente de una curva con la TI-84 Plus -
Añadir una línea tangente a un gráfico en TI-Nspire -
Calcular la pendiente de una función utilizando el cociente de diferencias -
Cómo determinar el costo marginal, el ingreso marginal y el beneficio marginal en la economía -
Cómo determinar si una función es discontinua
¿Cómo diferenciar funciones inversas Hay una fórmula difícil buscar la participación de las derivadas de las funciones inversas, pero antes de llegar a eso, a ver la figura siguiente, que resume muy bien la idea.Esta cifra muestra un par de funciones inversas, F y g. Funciones…
¿Cómo encontrar una línea normal a una curva Una línea normal a una curva en un punto dado es la línea perpendicular a la línea que es tangente en ese mismo punto. Encontrar los puntos de perpendicularidad para todas las líneas normales a la parábolaque pasan por el punto (3,…
¿Cómo encontrar una línea normal perpendicular a una recta tangente Una línea normal a una curva en un punto dado es la línea perpendicular a la línea que es tangente en ese mismo punto. Encontrar los puntos de perpendicularidad para todas las líneas normales a la parábolaque pasan por el punto (3,…
¿Cómo encontrar derivados de alto orden Encontrar un segundo, tercero, cuarto, o superior derivado es increíblemente simple. La segunda derivada de una función es simplemente la derivada de su primera derivada. La tercera derivada es la derivada de la segunda derivada, el cuarto…
¿Cómo encontrar los números críticos de una función Todos los extremos locales se producen en los puntos críticos de una función - que es donde la derivada es cero o indefinido (pero no se olvide que los puntos críticos no siempre son extremos locales). Así, el primer paso en la búsqueda de…
¿Cómo encontrar la derivada de una línea los derivado es sólo un término de cálculo de lujo para una idea simple que usted probablemente sabe de álgebra - pendiente. Slope es el término álgebra de lujo para la inclinación. Y lo escarpado es la palabra elegante para. . . ¡No! La…
¿Cómo encontrar las líneas tangentes de una parábola que pasan por un punto determinado ¿Alguna vez quiso determinar la ubicación de una línea a través de un punto dado que es tangente a una curva dada? Por supuesto que tienes! He aquí cómo lo haces.Determinar los puntos de tangencia de las líneas por el punto (1, -1) que son…
Cómo localizar intervalos de puntos de inflexión y concavidad Puede localizar la concavidad de una función (donde una función es cóncava hacia arriba o hacia abajo) y los puntos de inflexión (donde los interruptores concavidad de positivo a negativo o vice versa) en unos sencillos pasos. El siguiente…
Cómo hacer aproximaciones lineales Debido a que las funciones ordinarias son localmente lineal (que significa recto) - y cuanto más te acercas a ellos, el más recto que buscar-una línea tangente a una función es una buena aproximación de la función cerca del punto de…
El cociente de diferencias: el puente entre el álgebra (pendiente) y el cálculo (la derivada) Una de las piedras angulares de cálculo es el cociente de diferencias. El cociente de diferencias - junto con los límites - le permite tomar la fórmula pendiente edad ordinaria que utilizó para calcular la pendiente de las líneas en la clase de…
El teorema fundamental del cálculo El teorema fundamental del cálculo es uno de los teoremas más importantes en la historia de las matemáticas. Establece que, dada una función de área LAF que barre área bajo F (t),la velocidad a la que el área está siendo barrido es igual a…
Cómo determinar la medida de un ángulo cuyo vértice se encuentra fuera de un círculo Un ángulo que cruza un círculo puede tener su vértice en el interior, sobre o fuera del círculo. Este artículo aborda los tres tipos de ángulos que tienen sus vértices fuera de un círculo: ángulos secante-secantes, ángulos…