El teorema fundamental del cálculo

El teorema fundamental del cálculo es uno de los teoremas más importantes en la historia de las matemáticas. Establece que, dada una función de área LA_F que barre área bajo F (t),

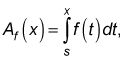
la velocidad a la que el área está siendo barrido es igual a la altura de la función original. Por lo tanto, porque la tasa es la derivada, la derivada de la función de área es igual a la función original:

Porque

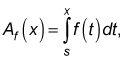
usted también puede escribir la ecuación anterior de la siguiente manera:

Romper las sales aromáticas.

Ahora, debido a la derivada de LA_F (X) es F (X), LA_F (X) Es por definición un antiderivada de F (X). Echa un vistazo a cómo funciona esto mirando una función simple, F (t) = 10, y su función de área,

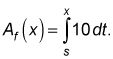
De acuerdo con el teorema fundamental,

Por lo tanto LA_F debe ser una primitiva de 10- en otras palabras, LA_F es una función cuya derivada es 10. Debido a que cualquier función de la forma 10X + C, dónde C es un número, ha un derivado de la 10, la primitiva de 10 es 10X + C. El número particular C depende de su elección de s, el punto donde se inicia barrer zona. Para una elección particular de s, la función de área será la función (de entre todas las funciones en la familia de curvas 10X + C) Que atraviesa el X-eje a s. Averiguar C, establecer el antiderivative igual a cero, el valor de enchufe s dentro X, y resuelve para C.

Para esta función con una antiderivada de 10X + C, si comienza a barrer la zona a, digamos,

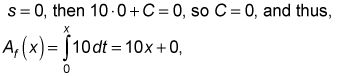
o simplemente 10X. (Tenga en cuenta que C no es necesariamente igual s. De hecho, por lo general no lo hace

Cuando s = 0, C a menudo también es igual a 0, pero no para todas las funciones.)

La cifra muestra por qué LA_F (X) = 10X es la función de área correcta si comienza a barrer la zona en cero.

fit; / i> (lt; i> TLT; / i>). = 10 "/>

En el gráfico superior en la figura, el área bajo la curva de 0 a 3 es 30, y que está dado por

Y se puede ver que la zona de 0 a 5 es 50, lo que concuerda con el hecho de que

Si en lugar de empezar a barrer la zona en s = -2 Y definir una nueva función de área,

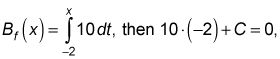
así C es igual a 20 y B_F (X) Es por lo tanto 10X + 20. Esta función área es 20 más que LA_F (X), Que comienza a las s = 0, porque si usted comienza a s = -2, Que ya ha arrastrado a cabo una superficie de 20 en el momento en que llegue a cero. La cifra muestra por qué B_F (3) es más de 20 LA_F (3).

Y si comienza a barrer la zona en

y la función de área es

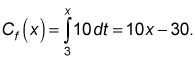
Esta función es 30 Menos de LA_F (X) Porque con C_F (X), Se pierde el rectángulo de 3 por 10 entre 0 y 3 que LA_F (X) Ha (véase el gráfico inferior de la figura).

Una función de zona es una antiderivada. El área barrida debajo de la línea horizontal F (t) = 10 desde algún número s a X, está dada por una antiderivada de 10, es decir 10X + C, donde el valor de C depende de por dónde empezar barriendo zona.

Ahora echa un vistazo a algunos de los gráficos LA_F (X), B_F (X), Y C_F (X).

(Tenga en cuenta que la cifra anterior no muestra las gráficas de LA_F (X), B_F (X), Y C_F (X). Verás tres gráficas de la función línea horizontal, F (t) = 10 y ves las áreas barridas bajo F (t) Por LA_F (X), B_F (X), Y C_F (X), Pero no se ve realmente las gráficas de estas tres funciones de área.)

El segundo gráfico muestra las gráficas de las ecuaciones de LA_F (X), B_F (X), Y C_F (X), Que ha trabajado antes: LA_F (X) = 10x, B_F (X) = 10X + 20, y C_F (X) = 10X - 30. (Como se puede ver, los tres son simples, y = mx + b líneas). La y-valores de estas tres funciones le dan las áreas barridas bajo F (t) = 10 que se ve en la primera figura. Tenga en cuenta que los tres X-intercepciones que se ven en la segunda figura son los tres X-valores en la primera figura en barrer comienza área.

Usted ya ha calculado que LA_F (3) = 30 y que LA_F (5) = 50. Se puede ver aquellas áreas de 30 y 50 en el gráfico superior de la primera figura. En la segunda figura, se ve estos resultados en LA_F en los puntos (3, 30) y (5, 50). También vio en la primera figura que B_F (3) fue de más de 20 LA_F (3) - que se ve que se traducen en la segunda figura en (3, 50) en B_F es superior a 20 (3, 30) en LA_F . Por último, se vio en la primera figura que C_F (X) Es menos de 30 LA_F (X). La segunda figura muestra que de una manera diferente: en cualquier X-valor, C_F la línea es de 30 unidades por debajo de la LA_F la línea.

Algunas observaciones. Usted ya sabe del teorema fundamental de que

(y lo mismo para B_F (X) Y C_F (X)). Eso se explicó anteriormente en términos de tasas: Para LA_F, B_F, y C_F, el índice de área que está siendo barrida bajo F (t) = 10 es igual a 10. La segunda figura también muestra que

(y lo mismo para B_F, y C_F), Pero aquí se ve el derivado como una pendiente. Las pendientes, por supuesto, de las tres líneas son iguales a 10. Por último, tenga en cuenta que las tres líneas en la segunda figura se diferencian entre sí únicamente por una traslación vertical. Estas tres líneas (y la infinidad de todas las demás líneas traducidas verticalmente) son todos los miembros de la clase de funciones, 10X + C, la familia de primitivas de F (X) = 10.