¿Cómo encontrar el área entre dos curvas
Para encontrar el área entre dos curvas, lo que necesita para llegar a una expresión para un rectángulo estrecho que se encuentra en una curva y sube a otro.
de X = 0 a X = 1:
Para obtener la altura del rectángulo de representación en la figura, restar el y-coordenada de su fondo de la y-coordenada de su parte superior - que es
Su base es el infinitesimal dx. Por lo tanto, debido a zona es igual a altura veces base,
Ahora que acaba de sumar las áreas de todos los rectángulos de 0 a 1 mediante la integración:
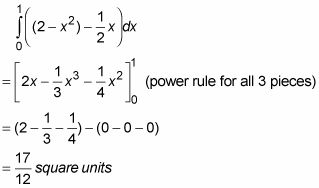
Ahora, para hacer las cosas un poco más retorcido, en el siguiente problema de las curvas se cruzan (ver la siguiente figura). Cuando esto sucede, usted tiene que dividir el total de área sombreada en regiones separadas antes de integrar. Pruebe esto:
de X = 0 a X = 2.
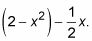
Determine donde las curvas se cruzan.
Cruzan en (1, 1) - lo que un asombroso casualidad! Así que tienes dos regiones separadas - una de 0 a 1 y otro 1-2.
Calcule el área de la región a la izquierda.
Calcule el área de la región a la derecha.
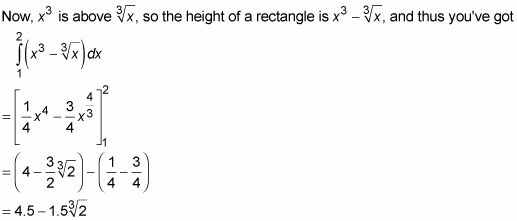
Sume las áreas de las dos regiones para conseguir la superficie total.
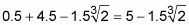
# 8776- 3.11 unidades cuadradas
Tenga en cuenta que la altura de un rectángulo representativo es siempre su cima menos su fondo, independientemente de si estos números son positivos o negativos. Por ejemplo, un rectángulo que va desde 20 hasta 30 tiene una altura de 30 - 20, o 10 un rectángulo que va desde -3 hasta 8 tiene una altura de 8 - (-3), o de 11 y un rectángulo que va desde -15 hasta -10 tiene una altura de -10 - (-15), o 5.
Si usted piensa acerca de este método top-menos-abajo para calcular la altura de un rectángulo, ahora se puede ver - suponiendo que no ya verlo - ¿por qué la integral definida de una función que cuenta el área por debajo de la X-eje negativo. Por ejemplo, considere la siguiente figura.
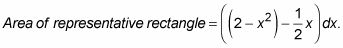
¿Cuál es la zona de sombra? Sugerencia: no es
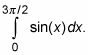
Si desea que la superficie total de la región sombreada que se muestra en la figura, hay que dividir la región sombreada en dos piezas separadas como lo hizo en el último problema.
Para la primera pieza, de 0 a pi, un rectángulo representante tiene una altura igual a la función en sí, y = Sen (X), Ya que su parte superior se encuentra en la función y su parte inferior está en cero - y, por supuesto, nada menos cero es en sí misma. De modo que el área de esta primera pieza está dada por lo común integral definida
la parte superior de un rectángulo representante está en cero - recordar que el X-eje es la línea y = 0 - y su parte inferior está en y = Sen (X), Por lo que su altura (dado, por supuesto, por la parte inferior, menos la parte superior) es 0 - sin (X), O simplemente -sen (X). Por lo tanto, para obtener el área de esta segunda pieza, a calcular la integral definida de la negativo de la función,
Porque esto negativo integrante le da la ordinaria, positivo área de la pieza por debajo de la X-eje, el positivo integral definida
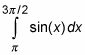
da una negativo zona. Es por eso que si usted calcula la integral definida
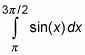
durante todo el período, la pieza debajo de la X-eje cuenta como un área negativa, y la respuesta que da el red de la zona superior de la X-eje menos el área por debajo del eje - en lugar de la zona de sombra totales. Claro como el barro?
Encuentra el área entre dos funciones Para encontrar un área entre dos funciones, es necesario establecer una ecuación con una combinación de integrales definidas de ambas funciones. Por ejemplo, suponga que desea calcular el área sombreada entre y = X2 ycomo se muestra en esta…
¿Cómo funciona la integración: es sólo Además de lujo El significado más fundamental de la integración es sumar. Y cuando representas la integración en un gráfico, se puede ver el proceso de sumar como un resumen de finas tiras rectangulares de área para llegar al área total bajo la curva, como…
Cómo estadísticas muestra la conexión entre la diferenciación y la integración Aún tratando de entender cómo el trabajo de diferenciación e integración? No hay problema: se puede usar las estadísticas para ayudarle. Mediante el estudio de la relación entre dos gráficos simples, vas a entender la relación entre la…
¿Cómo funciona la función de zona La función de zona es un poco extraño. Prepárate. Digamos que tienes una función de edad, F(t). Imagínese que en algún t-valor, lo llaman s, se dibuja una línea vertical fija. (Tenga en cuenta que debido a que esta línea es fijo, s es una…
Cómo aproximar el área del punto medio con rectángulos Una buena manera de aproximarse a las zonas con rectángulos es hacer que cada rectángulo cruzar la curva en el punto medio de la parte superior de ese rectángulo. Una suma punto medio es una mejor estimación del área que cualquiera a la…
Cómo aproximar área con la regla trapezoidal Con la regla trapezoidal, en lugar de aproximar el área mediante el uso de rectángulos (como lo hace con la izquierda, derecha, y los métodos de rectángulo del punto medio), su área aproximada con - ¿puedes adivinar? - Trapezoides.Debido a la…
Cómo hacer una aproximación área usando la notación sigma Notación Sigma es muy útil cuando se está aproximando el área bajo una curva. Por ejemplo, expresar una 8-derecha; aproximación rectángulo del área bajode 0 a 4 y calcular la aproximación.Expresa la idea básica de la suma:Esto sólo…
¿Cómo encontrar el valor medio de una función con el teorema del valor medio para integrales Usted puede encontrar el valor medio de una función en un intervalo cerrado usando el teorema del valor medio para integrales. La mejor manera de entender el teorema del valor medio es con un diagrama - echa un vistazo a continuación.El gráfico…
¿Cómo encontrar el valor medio con el teorema del valor medio para integrales Usted puede encontrar el valor medio de una función en un intervalo cerrado usando el teorema del valor medio para integrales. La mejor manera de entender el teorema del valor medio para integrales es con un diagrama - mira el siguiente figura.El…
¿Cómo medir el cambio de área bajo la curva Puede utilizar una función de área para medir el área bajo una curva, así como la zona cambios. Por ejemplo, digamos que usted tiene cualquier función de edad, F (t). Imagínese que en algún t-valor, lo llaman s, se dibuja una línea vertical…
Cómo dividir una integral definida en dos integrales definidas Cuando la solución de problemas de la zona, a veces es necesario dividir una integral en dos integrales definidas separadas. Aquí hay una regla simple, pero muy útil para hacer esto que parece complicado, pero es realmente muy fácil:Esta regla…
Determinar el área de un triángulo desde su base y la altura Si conoce la base y la altura de un triángulo, puede utilizar una fórmula probada y verdadera para encontrar su área. Es probable que primero encontró con la fórmula básica área del triángulo en aproximadamente sexto o séptimo grado. Si ha…