Cómo estadísticas muestra la conexión entre la diferenciación y la integración

Aún tratando de entender cómo el trabajo de diferenciación e integración? No hay problema: se puede usar las estadísticas para ayudarle. Mediante el estudio de la relación entre dos gráficos simples, vas a entender la relación entre la diferenciación y la integración (y, lo que es más, usted no necesita saber cualquier estadística en absoluto para comprender esta idea!).

Los gráficos en cuestión son un gráfico de distribución de frecuencias y un gráfico de distribución de frecuencia acumulativa (es posible que haya encontrado con este tipo de gráficos en un periódico o revista). Echa un vistazo a la figura.

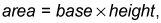
El gráfico superior de la figura muestra un histograma de distribución de frecuencias de las ganancias anuales de Widgets-R-Us del 1 de enero de 2001 hasta el 31 de diciembre de 2013. El rectángulo marcado '07, por ejemplo, muestra que el beneficio de la compañía para 2007 era $ 2.000.000 (su mejor año durante el período de 2001 hasta 2013).

El gráfico inferior en la figura es una acumulativo histograma de distribución de frecuencias para los mismos datos usados ​​para el gráfico superior. La diferencia es simplemente que en el gráfico acumulativa, la altura de cada columna muestra el total de los beneficios obtenidos desde 01.01.2001. Mira la columna de la '02 en el gráfico inferior y los '01 y '02 rectángulos en el gráfico superior, por ejemplo. Se puede ver que la columna muestra el '02 '02 rectángulo que se sienta encima del rectángulo '01 que da esa '02 columna de una altura igual al total de las ganancias de '01 y '02. ¿Lo tengo? A medida que avanza hacia la derecha en el gráfico acumulativo, la altura de cada columna sucesiva simplemente crece por la cantidad de beneficios obtenidos en el correspondiente año solo se muestra en el gráfico superior.

Bueno. Así que aquí está la conexión de cálculo. Mira el rectángulo superior de la columna de '08 en el gráfico acumulativo (llamémosle ese gráfico C para abreviar). En ese momento C, tú carrera a través de 1 año y subir hasta $ 1.250.000, el '08 de beneficio que se ve en el gráfico de distribución de frecuencias (F para abreviar). Cuesta abajo = subida / run, así, ya que la carrera es igual a 1, la pendiente es igual a 1.250.000 / 1, o simplemente 1.250.000, que es, por supuesto, la misma que la subida. Por lo tanto, la pendiente en C (en el '08 o cualquier otro año) puede leerse como una altura de F para el año correspondiente. (Asegúrese de ver cómo funciona esto.) Desde las alturas (o valores de la función) en F son los pendientes de C, F es el derivado de C. En breve, F, la derivada, le informa sobre la pendiente de C.

La siguiente idea es que desde F es la derivada de C, C, por definición, es la antiderivada de F (por ejemplo, C podría ser igual a 5X³ y F sería igual a 15X²). Ahora, lo que hace C, la antiderivada de F, decirte acerca de F? Imagínese arrastrando una línea vertical de izquierda a derecha sobre F. Como usted barre en los rectángulos de F - año por año - el beneficio total que está barriendo está demostrado subiendo a lo largo de C.

Mira las '01 a través '08 rectángulos en F. Usted puede ver esos mismos rectángulos subiendo escalón a lo largo de la moda C (ver los rectángulos marcados A, B, C, etc. en ambos gráficos). Las alturas de los rectángulos de F seguir sumando hasta el C a medida que suben la forma escalonada. Y usted ha visto cómo los mismos a través de '01 '08 rectángulos que se encuentran a lo largo de la parte superior de la escalera a paso de C También se puede ver en una pila vertical en años '08 en C. La gráfica acumulativa se extrae de esta manera por lo que es aún más evidente cómo las alturas de los rectángulos se suman. (Nota: La mayoría de los histogramas acumulativos no se extraen de esta manera.)

Cada rectángulo en F tiene una base de 1 año, por lo que, desde

el área de cada rectángulo es igual a su altura. Así que, como se comparan rectángulos en C, estás sumando las áreas de los rectángulos de F. Por ejemplo, la altura de la pila '08 '01 a través de rectángulos en C ($ 8,5 millones) es igual a la superficie total de los '01 a través de '08 rectángulos en F. Y, por tanto, las alturas o valores de la función de C - que es la antiderivada de F - le dará el área bajo el borde superior de F. Así es como funciona la integración.

Bueno, usted está casi terminado. Ahora vamos a ir a través de cómo estos dos gráficos explican la relación entre la diferenciación y la integración. Mira las '06 a través '12 rectángulos en F (con la frontera negrita). Usted puede ver esos mismos rectángulos en la parte en negrita de la columna de '12 de C. La altura de esa pila negrita, que muestra el total de los beneficios obtenidos durante esos 7 años, $ 7.750.000, es igual a la superficie total de los 7 rectángulos en F. Y para conseguir la altura de esa pila en C, sólo tiene que restar la altura del borde inferior de la pila desde la altura de su borde superior. Eso es realmente todo la versión de acceso directo del teorema fundamental dice: La zona en virtud de cualquier porción de una función (como F) Viene dada por el cambio en altura en antiderivada de la función (como C).

En pocas palabras (seguir buscando en los rectángulos con la frontera negrita en ambos gráficos), el pendientes de los rectángulos en C aparece como alturas en F. Eso es diferenciación. Inversión del sentido, que se ve integración: El cambio en alturas en C muestra el zona bajo F. Voil # 224-: la diferenciación y la integración son dos caras de la misma moneda.