La definición de la integral definida y cómo funciona

Usted puede aproximar el área bajo una curva mediante la suma de la derecha, izquierda o rectángulos punto medio. Para encontrar un área exacta, es necesario utilizar una integral definida.

Al aproximar el área bajo una curva, la parte superior de los rectángulos forman una forma de diente de sierra que no se ajusta a la perfección a lo largo de la función de curva suave. Por lo tanto, para encontrar el exacto área bajo una curva mediante rectángulos, que había necesidad de encontrar el área de un número infinito de rectángulos infinitamente delgadas cuya " tops " no encajar perfectamente la curva. Ahora, realmente no se puede utilizar un número infinito de rectángulos, pero con la invención fantástica de los límites, esto es una especie de lo que sucede.

Aquí está la " sencilla " definición de la integral definida que se utiliza para calcular las zonas exactas. Se basa en el límite de una suma de Riemann de rectángulos correctas. El área bajo una curva exacta entre la y b está dada por la integral definida, que se define como sigue:

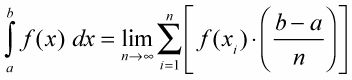
Al calcular una superficie aproximada o exacta bajo una curva, las tres sumas - izquierda, derecha, y el punto medio - se llaman sumas de Riemann después del gran matemático alemán GFB Riemann (1826 a 1866). Básicamente, cualquier cantidad formada por rectángulos es una suma de Riemann, incluidas las cantidades extrañas que consisten en rectángulos de anchura desigual.

Utilizando esta fórmula, aquí está el área exacta bajo X² + 1 entre 0 y 3:

Este resultado es bastante sorprendente si se piensa en ello. Utilizando el proceso de límite, se obtiene una exacto respuesta de 12 - que es algo así como 12,00000000 # 133- precisión de un número infinito de decimales - para el área bajo la función suave, curva, X² + 1, basándose en las áreas de rectángulos de cima plana que se ejecutan a lo largo de la curva en una, la moda de diente de sierra dentada.

Encontrar el área exacta de 12 utilizando el límite de una suma de Riemann es un montón de trabajo. Este complicado método de integración es comparable a la determinación de un derivado de la forma más dura con la definición formal que se basa en el cociente de diferencias. Y al igual que con el cociente de diferencias para encontrar un derivado, no utilizará el límite de una suma de Riemann para calcular el área una vez que aprender el método de acceso directo de encontrar el área.

Usted acaba de trabajar fuera del área bajo X² + 1, utilizando la fórmula para la suma de rectángulos correctas. (Por cierto, si usted va a calcular el área de la manera más dura con el límite de una suma de Riemann, que también podría utilizar siempre la derecha rectangles- es probablemente la forma más fácil de ir). Resulta, sin embargo, que podría haber utilizado rectángulos izquierda o rectángulos punto medio. De hecho, se podría haber utilizado una mezcla de diferentes tipos de rectángulos (no intente esto en casa). No importa qué tipo de rectángulos que utilice, el límite siempre sale lo mismo.

Esto le lleva a la siguiente hacia abajo y sucio jumbo totalmente extrema, Mumbo integración que toma todas estas posibilidades en cuenta. Es probable que nunca utiliza la siguiente definición de la integral definida. Así que ¿por qué debería aprenderlo? Buena pregunta. ¿Qué tal por la belleza de las matemáticas puras? O, si usted no compra eso y solamente está interesado en una razón práctica, casi la única motivación práctica para el aprendizaje de esta definición es que puede ser que sea en un examen.

La integral definida (definición real McCoy):