¿Cómo funciona la integración: es sólo Además de lujo

El significado más fundamental de la integración es sumar. Y cuando representas la integración en un gráfico, se puede ver el proceso de sumar como un resumen de finas tiras rectangulares de área para llegar al área total bajo la curva, como se muestra en esta figura.

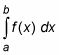
Usted puede calcular el área sombreada en la figura anterior mediante el uso de esta integral:

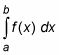
(Tenga en cuenta que todo lo que aquí implica definido en oposición a la integración indefinido la integración. La integración definitiva es donde la alargada S símbolo de la integración tiene límites de integración: los dos pequeños constantes o números en la parte inferior y la parte superior del símbolo. La alargada S sin límites de integración indica una indefinido o integral antiderivada.)

Mira el rectángulo delgado en la figura. Tiene una altura de F(X) Y una anchura de dx (un poco de X), Por lo que su área (largo veces ancho, por supuesto) viene dada por F(X) # 183- dx. La integral anterior le dice a sumar las áreas de todos los estrechos tiras rectangulares entre la y b bajo la curva F(X). A medida que las tiras consiguen más y más estrecho, se obtiene una estimación mejor y mejor de la zona. El poder de la integración radica en el hecho de que usted la da exacto área por tipo de sumar un número infinito de rectángulos infinitamente delgadas.

Independientemente de lo que los pequeños trozos son que usted está agregando para arriba - que podrían ser pequeños trozos de distancia o el volumen o la energía (o área justo) - se puede representar la suma como la suma de las áreas de tiras rectangulares delgadas bajo una curva . Si las unidades tanto en el X y y ejes son unidades de longitud, dicen, pies, luego cada delgadas medidas rectángulo tantos pies de tantos pies, y su área - largo veces ancho - es algún número de pies cuadrados. En este caso, el área total de todos los rectángulos entre la y b le da una respuesta de área (aunque no necesariamente el área real bajo la curva debido a que la escala puede ser diferente- por ejemplo, el área sombreada real en la figura de arriba se encuentra a pocos pulgadas cuadradas, pero su respuesta podría ser un número de millas cuadradas si ambos ejes fueron marcados fuera de millas). El punto es que en este caso, se agrega el áreas de todos los rectángulos, y se obtiene una zona responder. Por lo general, sin embargo, a pesar de realizar la suma de las áreas de rectángulos, su respuesta no será una respuesta zona.

Diga las unidades en el X-eje son horas (t) y el y-eje está etiquetado en millas por hora, entonces, porque tarifa veces hora es igual a distancia, el área de cada rectángulo representa una cantidad de la distancia y la superficie total que da la distancia total recorrida durante el intervalo de tiempo dado. O si el X-eje está etiquetado en horas (t) y el y-eje en kilovatios de energía eléctrica - en cuyo caso la curva, F(t), Da el uso de energía como una función del tiempo - a continuación, el área de cada tira rectangular (kilovatios veces horas) Representa un número de kilovatios-hora de energía. En ese caso, el área total bajo la curva que da el número total de kilovatios-hora de consumo de energía entre dos puntos en el tiempo.

Otra posibilidad se ilustra por la lámpara anteriormente. Digamos que usted desea calcular el volumen de la base de la lámpara. La siguiente figura muestra cómo se haría esto con la integración. En el gráfico, la función de LA(X) Da el área de sección transversal de una rebanada delgada pancake de la lámpara como una función de su altura medida desde el fondo de la lámpara. Así que esta vez, la h-eje está etiquetado en pulgadas (que es h como en altura desde la parte inferior de la lámpara), y el y-eje está etiquetado en pulgadas cuadradas, y por lo tanto cada rectángulo delgada tiene un ancho medido en pulgadas y una altura medida en pulgadas cuadradas. Su área, por lo tanto, representa pulgadas veces pulgadas cuadradas, o pulgadas cúbicas de volumen.

los zona del rectángulo delgado en esta figura representa la volumen de la rodaja delgada pancake de la lámpara 5 pulgadas desde la parte inferior de la base. El área total sombreada y por lo tanto el volumen de la base de la lámpara está dado por la siguiente integral:

Volumen = (área de sección transversal) veces (espesor)

Esto significa que se suman los volúmenes de todas las rebanadas delgadas tortitas de 0 a 15 pulgadas (es decir, desde la parte inferior a la parte superior de la base de la lámpara), cada rebanada tiene un volumen dado por LA(h) (Su área transversal) veces dh (su altura o espesor).

En resumen - que es un juego de palabras! - La expresión matemática a la derecha de cualquier símbolo integración definida siempre significa un poco de algo, y la integración de tal expresión significa sumar todas las pequeñas piezas entre un cierto punto de partida y un punto final para determinar el total entre los dos puntos .