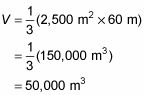¿Cómo se mide en tres dimensiones

Medición en tres dimensiones es similar a la medición en dos dimensiones sin embargo, en 3-D, el límite de un sólido se llama su área de superficie

(no su perímetro) Y lo que es el interior de un sólido se llama su volumen (no su área).

El área de superficie de un sólido es una medida del tamaño de su superficie, tal como se mide en unidades cuadradas, como pulgadas cuadradas (en.²), Pies cuadrados (ft.²), Metros cuadrados (m²), etcetera. El volumen (V) De un sólido es una medida del espacio que ocupa, tal como se mide en unidades cúbicas tales como pulgadas cúbicas (pulg.³), De pies cúbicos (ft.³), Metros cúbicos (m³), etcetera.

Esferas de medición

El centro de una esfera es un punto que es la misma distancia desde cualquier punto de la esfera en sí. Esta distancia se denomina radio (r) De la esfera. Si conoce el radio de una esfera, puede averiguar su volumen utilizando la siguiente fórmula:

Debido a que esta fórmula incluye # 112-, utilizando 3,14 como valor aproximado para # 112- le da una aproximación del volumen. Por ejemplo, aquí está cómo averiguar el volumen aproximado de una pelota cuyo radio es de 4 pulgadas:

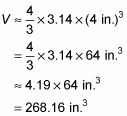
(Nota: En el problema anterior, se utiliza signos igual cuando un valor es igual a lo que viene justo antes de él y, aproximadamente, igual a signos () al año.)

Cubos de medición

La medición principal de un cubo es la longitud de su lado (s). El uso de esta medida, se puede averiguar el volumen de un cubo con la siguiente fórmula:

V = s³

Así que si el lado de un cubo es de 5 metros, así es como a determinar su volumen:

V = (5 m)³ = 5 m 5 m 5 m = 125 m³

Puedes leer 125 m³ como 125 metros cúbicos o, con menor frecuencia, como 125 metros en cubos.

Cajas de medida (sólidos rectangulares)

Las tres medidas de una caja (o sólido rectangular) son su longitud (l), Anchura (w), Y la altura (h). El cuadro representado en la figura de abajo tiene las siguientes medidas:

l = 4 m, w = 3 m, y h = 2 m.

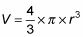
Usted puede encontrar el volumen de una caja con la siguiente fórmula:

V = l w h

Así que aquí es cómo encontrar el volumen de la caja de la foto de arriba:

V = 4 m 3 m 2 m = 24 m³

Prismas de medición

Encontrar el volumen de un prisma es fácil si usted tiene dos mediciones. Una medida es la altura (h) Del prisma. El segundo es el área de la base (LA_b). La base es el polígono que se extiende verticalmente desde el plano.

Aquí está la fórmula para encontrar el volumen de un prisma:

V = A_b h

Por ejemplo, supongamos que un prisma tiene una base con una superficie de 5 centímetros cuadrados y una altura de 3 centímetros. He aquí cómo usted encuentra su volumen:

V = 5 cm² 3 cm = 15 cm³

Tenga en cuenta que las unidades de medida (cm² y cm) también se multiplica, que le da un resultado de cm³.

Cilindros de medición

Usted encuentra el volumen de cilindros de la misma forma que le parezca el área de prismas - multiplicando el área de la base (LA_b) Por el cilindro de altura (h):

V = LA_b h

Suponga que usted desea encontrar el volumen de una lata cilíndrica cuya altura es de 4 pulgadas y cuya base es un círculo con un radio de 2 pulgadas. En primer lugar, encontrar el área de la base mediante el uso de la fórmula para el área de un círculo:

LA_b = # 112- r²

3,14 (2 in.)²

= 3.14 4 en.²

= 12,56 en.²

Esta zona es aproximada porque usas 3,14 como valor aproximado para # 112-.

Ahora usa esta área para encontrar el volumen del cilindro:

V 12.56 in.² 4 pulg. = 50,24 en.³

Observe cómo multiplicar pulgadas cuadradas (in.²) Por pulgadas da un resultado en pulgadas cúbicas (pulg.³).

Pirámides y conos de medición

Las dos medidas clave para pirámides y conos son los mismos que aquellos para los prismas y cilindros: la altura (h) Y el área de la base (LA_b). Aquí está la fórmula para el volumen de una pirámide o un cono:

Por ejemplo, suponga que desea encontrar el volumen de un cono de helado cuya altura es de 4 pulgadas y cuya área de la base es de 3 pulgadas cuadradas. He aquí cómo se hace:

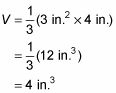
Del mismo modo, supongamos que usted desea encontrar el volumen de una pirámide en Egipto, cuya altura es de 60 metros con una base cuadrada cuyos lados son cada 50 metros. En primer lugar, encontrar el área de la base:

LA_b = s² = (50 m)² = 2,500 m²

Ahora usa esta área para encontrar el volumen de la pirámide: