Cómo utilizar el método Shell para medir el volumen de un sólido
los método de shell permite medir el volumen de un sólido mediante la medición del volumen de muchas superficies concéntricas de volumen, llamado " conchas ". Aunque el método de shell funciona sólo para sólidos con secciones transversales circulares, es ideal para sólidos de revolución alrededor del y-eje, porque usted no tiene que utilizar inversas de funciones.
Así es como funciona:
Encuentra una expresión que representa el área de una concha aleatoria del sólido en términos de X.
Utilice esta expresión para construir una integral definida (en términos de dx) Que representa el volumen del sólido.
Evaluar esta integral.
Usted puede usar una lata de sopa - o cualquier otra lata que tiene una etiqueta de papel en él - como ayuda visual útil para darle una idea de cómo funciona el método de shell. Para empezar, vaya a la despensa y conseguir una lata de sopa.
Suponga que su lata de sopa es de tamaño industrial, con un radio de 3 pulgadas y una altura de 8 pulgadas. Puede utilizar la fórmula para un cilindro de averiguar el volumen de la siguiente manera:
V = LAb # 183- h = 32# 960- # 183- 8 = 72 # 960;
También puede utilizar el método de la cáscara, que se muestra aquí.
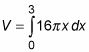
Para entender el método de cáscara, cortar etiqueta de papel de la lata en posición vertical, y retire con cuidado de la lata, como se muestra en la figura. (Mientras estás en ello, tome un momento para leer la etiqueta para que no te queda " sopa de misterio ").
Observe que la etiqueta no es más que un rectángulo. Su lado más corto es de longitud igual a la altura de la lata (8 pulgadas) y su lado más largo es igual a la circunferencia (2# 960- # 183- 3 pulgadas = 6# 960- pulgadas). De modo que el área de este rectángulo es 48# 960- pulgadas cuadradas.
Ahora aquí está el paso crucial: Imagina que toda la lata se compone de un número infinito de etiquetas envueltos concéntricamente alrededor de la otra, todo el camino hasta su núcleo. El área de cada uno de estos rectángulos es:
LA = 2# 960- X 183- # 8 = 16# 960- X
La variable X en este caso es cualquier radio posible, de 0 (el radio del círculo en el centro mismo de la lata) a 3 (el radio del círculo en el borde exterior). He aquí cómo se utiliza el método de shell, paso a paso, para encontrar el volumen de la lata:
Encuentra una expresión que representa el área de una concha aleatoria de la lata (en términos de X):
LA = 2# 960- X 183- # 8 = 16# 960- X
Utilice esta expresión para construir una integral definida (en términos de dx) Que representa el volumen de la lata.
Recuerde que con el método de concha, que está sumando todas las conchas del centro (donde el radio es 0) hasta el borde exterior (donde el radio es 3). Así que utilice estos números como los límites de integración:
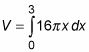
Evaluar esta integral:
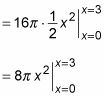
Ahora evaluar esta expresión:
= 8# 960- (3)2 - 0 = 72# 960-
El método shell verifica que el volumen de la lata es 72# 960- pulgadas cúbicas.
-
Conceptos de geometría a su estudiante de la escuela secundaria deben conocer las normas básicas comunes -
¿Cómo se mide en tres dimensiones -
Encontrar el volumen de un sólido con secciones transversales congruentes -
Encontrar el volumen de un sólido con secciones transversales similares -
Encontrar volumen con el método de muñecas matryoshka (aka El método carcasa cilíndrica) -
Encontrar el volumen de un sólido utilizando el método de disco
¿Cómo funciona la integración: es sólo Además de lujo El significado más fundamental de la integración es sumar. Y cuando representas la integración en un gráfico, se puede ver el proceso de sumar como un resumen de finas tiras rectangulares de área para llegar al área total bajo la curva, como…
¿Cómo evaluar el volumen de un sólido de revolución Puede evaluar el volumen de un sólido de revolución. Un sólido de revolución se crea mediante la adopción de una función, o parte de una función, y girando alrededor de un eje - en la mayoría de los casos, ya sea la X-eje o la y-eje.Un…
¿Cómo encontrar el volumen de una forma circular con el método de la integración pila-de-panqueques Geometría te dice cómo calcular los volúmenes de sólidos sencillos. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas. La técnica de pila-de-panqueques funciona cuando las secciones…
¿Cómo encontrar el volumen de una forma cilíndrica con el método anidados-ruso-muñecas de la integración Integración que permite calcular los volúmenes de una infinita variedad de formas complicadas que no se puede manejar con una geometría regular. Usted puede cortar un sólido en cilindros concéntricos delgadas y luego sumar los volúmenes de…
¿Cómo encontrar el volumen de una forma utilizando el método de la arandela de la integración Geometría te dice cómo calcular los volúmenes de sólidos sencillos. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas. Si usted tiene una forma circular con un agujero circular en el…
¿Cómo encontrar el volumen de una forma utilizando el método de la arandela Geometría te dice cómo calcular los volúmenes de sólidos sencillos. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas. Si usted tiene una forma redonda con un agujero en el centro, se…
¿Cómo encontrar el volumen de un sólido entre dos superficies de revolución Si desea encontrar el volumen de un sólido que se encuentra entre dos superficies distintas de la revolución, puede utilizar el método de carne máquina de cortar para hacer esto. los Método de carne máquina de cortar funciona mejor con los…
Cómo medir el volumen de un sólido de forma irregular Se puede medir el volumen de cualquier sólido con una sección transversal que es una función de de forma irregular X. En algunos casos, estos sólidos son más difíciles de describir de lo que son para medir. Por ejemplo, echar un vistazo a esta…
¿Cómo medir el volumen de un objeto al convertirlo en su lado A veces, si se desea medir el volumen de un objeto, es necesario convertirla en su lado de modo que usted puede utilizar el método de carne máquina de cortar. Este método funciona mejor con los sólidos que tienen secciones transversales…
La medición de volumen bajo una superficie usando una integral doble Una integral doble le permite medir el volumen bajo una superficie tan limitada por un rectángulo. Integrales definidas proporcionan una forma confiable de medir el área firmado entre una función y la X-eje como limitada por cualquiera de los dos…
Medición del volumen de una pirámide Suponga que usted desea encontrar el volumen de una pirámide de base cuadrada de 6 x 6 unidades y una altura de 3 unidades. Geometría le dice que usted puede utilizar la siguiente fórmula:Esta fórmula funciona muy bien, pero no te da una idea de…
Radio, diámetro, circunferencia, y el área de círculos LA círculo es una figura geométrica que necesita sólo dos piezas que lo identifican y clasifican: su centro (o medio) y su radio (la distancia desde el centro hasta cualquier punto en el círculo). Después de elegir un punto para ser el centro…