¿Cómo encontrar el volumen de un sólido entre dos superficies de revolución
Si desea encontrar el volumen de un sólido que se encuentra entre dos superficies distintas de la revolución, puede utilizar el método de carne máquina de cortar para hacer esto. los Método de carne máquina de cortar funciona mejor con los sólidos que tienen secciones transversales similares. Este es el plan:
Encuentra una expresión que representa el área de una sección transversal al azar del sólido en términos de X.
Utilice esta expresión para construir una integral definida (en términos de dx) Que representa el volumen del sólido.
Evaluar esta integral.
El truco es encontrar una manera de describir la zona en forma de anillo de una sección transversal como la diferencia entre dos integrales: un integrante que describe toda la forma menos otro que describe el agujero.
Por ejemplo, supongamos que usted desea encontrar el volumen del sólido que se muestra aquí.
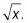
Este aspecto sólidos algo así como un tazón volvió a su lado. El borde exterior es el sólido de revolución alrededor del X-eje para la función de
El borde interior es el sólido de revolución alrededor del X-eje para la función de
Aquí está la manera de resolver este problema:
Encuentra una expresión que representa el área de una sección transversal al azar del sólido.
Es decir, encontrar el área de un círculo con un radio de
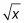
y restar el área de un círculo con un radio de
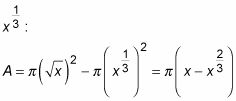
Utilice esta expresión para construir una integral definida que representa el volumen del sólido.
Los límites de integración son 0 y 4:
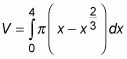
Resuelve la integral:
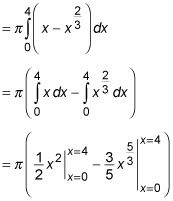
Ahora evaluar esta expresión:
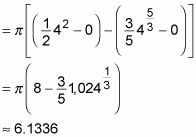
Aquí hay otro problema: Encontrar el volumen del sólido que se muestra aquí.
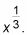
Este sólido caídas entre la superficie de revolución y = Ln X y la superficie de revolución
limitada hacia abajo por y = 0 y por encima de por y = 1.
La sección transversal de este sólido se muestra a la derecha; lado de la figura: un círculo con un agujero en el centro.
Nótese, sin embargo, que esta sección transversal es perpendicular a la y-eje. Para utilizar el método de carne máquina de cortar, la sección transversal debe ser perpendicular a la X-eje. Modificar el problema utilizando inversas:
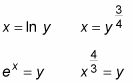
El problema resultante se muestra en esta figura.
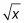
Ahora usted puede utilizar el método de carne máquina de cortar para resolver el problema:
Encuentra una expresión que representa el área de una sección transversal al azar del sólido.
Es decir, encontrar el área de un círculo con un radio de eX y restar el área de un círculo con un radio de
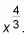
Esta es la geometría justa. Recuerde que el área de un círculo es # 960-r2:
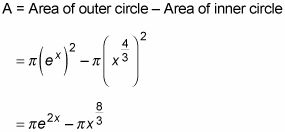
Utilice esta expresión para construir una integral definida que representa el volumen del sólido.
Los límites de integración son 0 y 1:
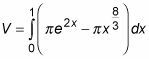
Evaluar la integral:
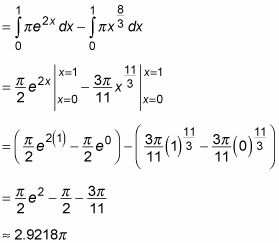
Por lo tanto el volumen de este sólido es de aproximadamente 9.179 unidades cúbicas.
-
¿Cómo se mide en tres dimensiones -
Encontrar el área de una superficie de revolución -
Encontrar el volumen de un sólido con secciones transversales congruentes -
Encontrar el volumen de un sólido con secciones transversales similares -
Encontrar volumen con el método de muñecas matryoshka (aka El método carcasa cilíndrica) -
Encontrar el volumen de un sólido utilizando el método de disco
¿Cómo funciona la integración: es sólo Además de lujo El significado más fundamental de la integración es sumar. Y cuando representas la integración en un gráfico, se puede ver el proceso de sumar como un resumen de finas tiras rectangulares de área para llegar al área total bajo la curva, como…
¿Cómo evaluar el volumen de un sólido de revolución Puede evaluar el volumen de un sólido de revolución. Un sólido de revolución se crea mediante la adopción de una función, o parte de una función, y girando alrededor de un eje - en la mayoría de los casos, ya sea la X-eje o la y-eje.Un…
¿Cómo encontrar el área de volumen y superficie del cuerno de gabriel Encontrar el área de volumen y superficie de este problema bocina puede volar tu mente. Cuerno de Gabriel es el sólido generado al girar sobre el X-eje de la región sin límites entreEsta cifra muestra un gráfico del cuerno de Gabriel.Jugar este…
¿Cómo encontrar el volumen de una forma circular con el método de la integración pila-de-panqueques Geometría te dice cómo calcular los volúmenes de sólidos sencillos. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas. La técnica de pila-de-panqueques funciona cuando las secciones…
¿Cómo encontrar el volumen de una forma complicada con el método de carne máquina de cortar de la integración En geometría, usted aprendió cómo calcular los volúmenes de sólidos simples como cajas, cilindros y esferas. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas.La metáfora de carne…
¿Cómo encontrar el volumen de una forma cilíndrica con el método anidados-ruso-muñecas de la integración Integración que permite calcular los volúmenes de una infinita variedad de formas complicadas que no se puede manejar con una geometría regular. Usted puede cortar un sólido en cilindros concéntricos delgadas y luego sumar los volúmenes de…
¿Cómo encontrar el volumen de una forma utilizando el método de la arandela de la integración Geometría te dice cómo calcular los volúmenes de sólidos sencillos. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas. Si usted tiene una forma circular con un agujero circular en el…
¿Cómo encontrar el volumen de una forma utilizando el método de la arandela Geometría te dice cómo calcular los volúmenes de sólidos sencillos. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas. Si usted tiene una forma redonda con un agujero en el centro, se…
Cómo medir el volumen de un sólido de forma irregular Se puede medir el volumen de cualquier sólido con una sección transversal que es una función de de forma irregular X. En algunos casos, estos sólidos son más difíciles de describir de lo que son para medir. Por ejemplo, echar un vistazo a esta…
¿Cómo medir el volumen de un objeto al convertirlo en su lado A veces, si se desea medir el volumen de un objeto, es necesario convertirla en su lado de modo que usted puede utilizar el método de carne máquina de cortar. Este método funciona mejor con los sólidos que tienen secciones transversales…
Cómo utilizar el método Shell para medir el volumen de un sólido los método de shell permite medir el volumen de un sólido mediante la medición del volumen de muchas superficies concéntricas de volumen, llamado " conchas ". Aunque el método de shell funciona sólo para sólidos con secciones transversales…
La medición de volumen bajo una superficie usando una integral doble Una integral doble le permite medir el volumen bajo una superficie tan limitada por un rectángulo. Integrales definidas proporcionan una forma confiable de medir el área firmado entre una función y la X-eje como limitada por cualquiera de los dos…