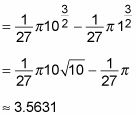Encontrar el área de una superficie de revolución
Lo bueno de hallar el área de una superficie de revolución es que no hay una fórmula que puede utilizar. Memorizarlo y ya está a medio camino hecho.
Para encontrar el área de una superficie de revolución entre la y b, utilizar la siguiente fórmula:
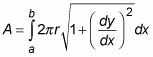
Esta fórmula es largo y complicado, pero tiene más sentido cuando pasas un minuto pensando en ello. La integral se hace de dos piezas:
La fórmula longitud de arco, que mide la longitud a lo largo de la superficie
La fórmula para la circunferencia de un círculo, que mide la longitud alrededor de la superficie
Así multiplicando estas dos piezas juntas es similar a la multiplicación de longitud y anchura para encontrar el área de un rectángulo. En efecto, la fórmula permite medir la superficie como un número infinito de pequeños rectángulos.
Cuando usted está midiendo la superficie de revolución de una función F(X) alrededor de X-eje, sustituto r = F(X) En la fórmula:
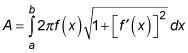
Por ejemplo, suponga que desea para encontrar el área de la revolución que se muestra en esta figura.
Para resolver este problema, primero en cuenta que para
Así que configurar el problema de la siguiente manera:
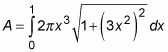
Para empezar, simplificar el problema un poco:
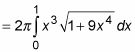
Puede resolver este problema utilizando la siguiente sustitución de variables:
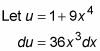
Ahora sustituir u para 1+ 9X4 y
para X3 dx en la ecuación:
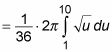
Observe que cambia los límites de integración: Cuando X = 0, u = 1. Y cuando X = 1, u = 10.
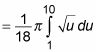
Ahora usted puede realizar la integración:
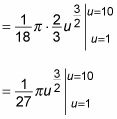
Por último, evaluar la integral definida:
¿Cómo evaluar el volumen de un sólido de revolución Puede evaluar el volumen de un sólido de revolución. Un sólido de revolución se crea mediante la adopción de una función, o parte de una función, y girando alrededor de un eje - en la mayoría de los casos, ya sea la X-eje o la y-eje.Un…
¿Cómo encontrar el área de una superficie de revolución Una superficie de revolución es una superficie en tres dimensiones con secciones transversales circulares, como un florero o una campana o una botella de vino. Para estos problemas, se divide la superficie en bandas circulares estrechos, calcular…
¿Cómo encontrar el volumen de un sólido entre dos superficies de revolución Si desea encontrar el volumen de un sólido que se encuentra entre dos superficies distintas de la revolución, puede utilizar el método de carne máquina de cortar para hacer esto. los Método de carne máquina de cortar funciona mejor con los…
Cómo utilizar el método Shell para medir el volumen de un sólido los método de shell permite medir el volumen de un sólido mediante la medición del volumen de muchas superficies concéntricas de volumen, llamado " conchas ". Aunque el método de shell funciona sólo para sólidos con secciones transversales…
La medición de volumen bajo una superficie usando una integral doble Una integral doble le permite medir el volumen bajo una superficie tan limitada por un rectángulo. Integrales definidas proporcionan una forma confiable de medir el área firmado entre una función y la X-eje como limitada por cualquiera de los dos…
Medición del volumen de una pirámide Suponga que usted desea encontrar el volumen de una pirámide de base cuadrada de 6 x 6 unidades y una altura de 3 unidades. Geometría le dice que usted puede utilizar la siguiente fórmula:Esta fórmula funciona muy bien, pero no te da una idea de…
Solución de problemas de integración en el cálculo Cálculo acertijo: ¿Qué teorema del valor medio, la lavadora y Métodos de Shell, y la longitud del arco y de la superficie de las fórmulas de la revolución tienen en común? Todos ellos implican la integración. La integración es además muy…
La definición de la integral definida y cómo funciona Usted puede aproximar el área bajo una curva mediante la suma de la derecha, izquierda o rectángulos punto medio. Para encontrar un área exacta, es necesario utilizar una integral definida.Al aproximar el área bajo una curva, la parte superior…
Determinar el área de un triángulo desde su base y la altura Si conoce la base y la altura de un triángulo, puede utilizar una fórmula probada y verdadera para encontrar su área. Es probable que primero encontró con la fórmula básica área del triángulo en aproximadamente sexto o séptimo grado. Si ha…
La determinación de la superficie de un triángulo equilátero Para calcular el área de un triángulo - para la mayoría de tipos de triángulos - lo que necesita saber de base y la altura del triángulo. Sin embargo, con un triángulo equilátero, todo lo que necesitas saber es la longitud de uno de sus…
Cómo determinar el área de sectores y segmentos de un círculo Marque una sección de un círculo con un arco y una cuerda, y usted tiene un segmento (este tipo de segmento tiene nada que ver con un segmento de línea). Lanzar un par de radios alrededor de un arco, y usted tiene un sector.Así que aquí están…
Fórmulas de geometría famosos que usted debe saber para el ASVAB Las subpruebas de matemáticas del ASVAB menudo piden que utilizar fórmulas básicas de geometría para calcular mediciones geométricas. Usted debe comprometerse estas fórmulas simples para la memoria si usted está esperando para una puntuación…