Encontrar el área de un triángulo utilizando sus coordenadas
La primera fórmula más encuentro para encontrar el área de un triángulo es LA = 1frasl-2bh. Para utilizar esta fórmula, es necesario que la medida de un solo lado del triángulo, más la altura del triángulo (perpendicular a la base), elaborado a partir de ese lado. El triángulo de abajo tiene una superficie de LA = 1frasl-2(6) (4) = 12 unidades cuadradas.
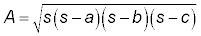
Encontrar una medida perpendicular no siempre es conveniente, especialmente si usted está calculando el área de un gran trozo triangular de la tierra, por lo que la fórmula de Herón se puede utilizar para encontrar el área de un triángulo cuando se tiene las medidas de los tres lados. Utiliza la fórmula de Herón el semi-perímetro (la mitad del perímetro) y las medidas de los tres lados:
dónde s es la semi-perímetro y la, b, y c son las medidas de los lados. Encontrar el área del triángulo a continuación:
(Por supuesto, esto es un triángulo rectángulo, por lo que sólo podía usar los dos lados perpendiculares como base y la altura.)
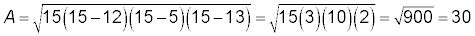
Ahora, considere un triángulo que se representa gráficamente en el plano de coordenadas. Siempre se puede utilizar la fórmula de la distancia, encontrar las longitudes de los tres lados, y luego aplicar la fórmula de Herón. Pero hay una mejor opción, basada en el determinante de una matriz. Aquí está una fórmula de utilizar, sobre la base de la entrada en sentido antihorario de las coordenadas de los vértices del triángulo (X1, y1), (X2, y2), (X3, y3) O (2, 1), (8, 9), (1, 8): LA = X1y2 + X2y3 + X3y1 - X1y3 - X2y1 - X3y2.
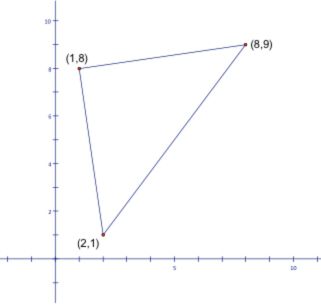
Comenzando con el punto (2, 1) y en sentido antihorario, LA = 2 (9) + 8 (8) + 1 (1) - 2 (8) - 8 (1) - 1 (9) = 18 + 64+ 1 - 16 a 8 - 9 = 83 - 33 = 50. El área del triángulo es de 50 unidades cuadradas.
Encontrar la altitud de un triángulo La altitud de un triángulo es un segmento de un vértice del triángulo hacia el lado opuesto (o a la extensión del lado opuesto si es necesario) que es perpendicular a la opuesta lateral del lado opuesto se llama la base. (Se utiliza la…
Cómo calcular el área de un hexágono regular Una forma de encontrar el área de un hexágono regular es de primera división en triángulos equiláteros. También es necesario utilizar un apotema - un segmento que une el centro de un polígono regular hasta el punto medio de cualquier lado y…
Cómo calcular el área de un polígono regular LA polígono regular es equilátero (tiene lados iguales) y equiangular (tiene ángulos iguales). Para encontrar el área de un polígono regular, se utiliza un apotema - un segmento que une el centro del polígono al punto medio de cualquier lado y…
La identificación de triángulos por sus ángulos Se puede clasificar triángulos por sus ángulos, así como por sus lados. Las clasificaciones basadas en ángulos son como sigue:Triángulo aguda: Un triángulo con tres ángulos agudos (menos de 90 # 176-).Triángulo obtuso: Un triángulo con un…
Triángulos trigonométricas básicas Todo por su cuenta, los ángulos son sin duda muy emocionante. Pero los puso en un triángulo, y usted tiene la guinda del pastel. Triángulos son una de las figuras geométricas estudiadas con más frecuencia. Los ángulos que forman el triángulo…
Encuentre el área de un triángulo con asa Cuando se tienen dos ángulos en un triángulo y el lado entre ellos (ASA), puede utilizar trigonométrica para hallar el área del triángulo. Las fórmulas van como sigue.En el triángulo Abecedario, si las medidas de los lados son la, b, y c…
Cómo circunscribir un triángulo Cada triángulo puede ser circunscrito por un círculo, lo que significa que un círculo - y sólo uno - pasa por los tres vértices (esquinas) de cualquier triángulo. En términos de los laicos, cualquier triángulo puede encajar en algún…
¿Cómo encontrar el área de un triángulo para sss según la fórmula de la garza Puede utilizar la fórmula de Herón para calcular el área del triángulo, incluso si sólo se sabe de los lados del triángulo y no cualquiera de los ángulos (que se llama SSS, o de lado de lado a lado, en términos de trigonometría). La…
¿Cómo encontrar el área de un triángulo con sas Cuando usted sabe las longitudes de dos de los lados de un triángulo más la medida del ángulo entre los lados (SAS), se encuentra el área del triángulo. Este método requiere un poco de trigonometría - usted tiene que encontrar el seno del…
Cómo localizar el centro de un triángulo Si dibuja líneas de cada esquina (o vértice) De un triángulo para el punto medio de los lados opuestos, entonces esas tres líneas se encuentran en un centro, o centroide, del triángulo. El centro de gravedad es el centro del triángulo de la…
Cómo utilizar la fórmula de Herón para calcular el área de un triángulo Usted puede encontrar el área de un triángulo utilizando la fórmula de Herón. Fórmula de Herón es especialmente útil cuando se tiene acceso a las medidas de los tres lados de un triángulo, pero no puede dibujar una altura perpendicular o no…
Cómo usar la trigonometría para encontrar el área de un triángulo A veces, la búsqueda de una medida que no es tan fácil. Puede que tenga que hacer frente a una forma irregular, como un triángulo, o incluso calcular su camino alrededor de un objeto fijo. En cualquier caso, puede utilizar la trigonometría para…