¿Cómo encontrar el área de un triángulo para sss según la fórmula de la garza
Puede utilizar la fórmula de Herón para calcular el área del triángulo, incluso si sólo se sabe de los lados del triángulo y no cualquiera de los ángulos (que se llama SSS, o de lado de lado a lado, en términos de trigonometría). La fórmula de Herón es muy útil, por ejemplo, si usted necesita para encontrar el área máxima posible dada la suma de los lados de un triángulo.
Por ejemplo, suponga que tiene 240 yardas de la esgrima, y usted decide construir un corral triangular para su llama. ¿Por triangular? Ya has oído que las llamas favorecen la forma, por supuesto. Usted quiere que la llama que tiene suficiente espacio para correr, por lo que necesita para conocer la zona. ¿Cuáles deberían ser las longitudes de los lados del triángulo? Puede resolver este pequeño problema mediante el uso de la fórmula de Herón para el área de un triángulo.
La fórmula de Herón dice que si un triángulo Abecedario tiene lados de longitudes la, b, y c frente a los respectivos ángulos, y deja que el semiperímetro, s, representan la mitad del perímetro del triángulo, entonces el área del triángulo es
En el problema de la esgrima y la llama, usted tiene muchas maneras de hacer un triangular corral de 240 yardas de la esgrima. La siguiente figura muestra algunas de las posibilidades. Observe que, en cada caso, las longitudes de los lados se suman a 240. Por el bien de este problema, no se preocupe por una puerta.
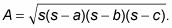
Qué triángulo tiene la mayor área? Obviamente, uno de ellos es un poco en el lado flaco, a pesar de que utiliza hasta 240 yardas de la esgrima, como los demás. Aquí está la manera de calcular las áreas de los tres triángulos.
Encuentra el semiperímetro, s, para cada triángulo.
En referencia a la figura anterior:
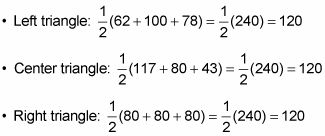
No en vano, todos los semiperimeters son los mismos, ya que todos los perímetros son 240.
Utilice Fórmula de Herón para encontrar cada área.
Una vez más, refiriéndose a la figura anterior:
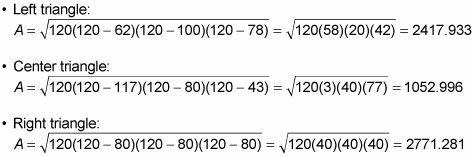
El triángulo de la derecha tiene la mayor área. De las formas en la figura, ese triángulo es el mejor. Pero usted puede preguntarse si otra forma da más superficie que esa. La respuesta: no. Con cálculo, se puede demostrar que un triángulo equilátero le da la mayor área posible con cualquier cantidad de esgrima. Sin cálculo, sólo tienes que probar un montón de formas de convencer a ti mismo.
La determinación de la superficie de un triángulo equilátero Para calcular el área de un triángulo - para la mayoría de tipos de triángulos - lo que necesita saber de base y la altura del triángulo. Sin embargo, con un triángulo equilátero, todo lo que necesitas saber es la longitud de uno de sus…
Encontrar la altitud de un triángulo La altitud de un triángulo es un segmento de un vértice del triángulo hacia el lado opuesto (o a la extensión del lado opuesto si es necesario) que es perpendicular a la opuesta lateral del lado opuesto se llama la base. (Se utiliza la…
Cómo calcular el área de un hexágono regular Una forma de encontrar el área de un hexágono regular es de primera división en triángulos equiláteros. También es necesario utilizar un apotema - un segmento que une el centro de un polígono regular hasta el punto medio de cualquier lado y…
Cómo calcular el área de un polígono regular LA polígono regular es equilátero (tiene lados iguales) y equiangular (tiene ángulos iguales). Para encontrar el área de un polígono regular, se utiliza un apotema - un segmento que une el centro del polígono al punto medio de cualquier lado y…
Cómo calcular el área de un cometa Usted calcula el área de un cometa mediante el uso de las longitudes de sus diagonales. He aquí un ejemplo: ¿cuál es el área de la cometa COMETA en la siguiente figura?Para los problemas de la cometa zona (y algunas veces otros problemas…
Cómo calcular el área de un paralelogramo, cometa, o trapezoidal Las fórmulas del área para el paralelogramo, cometa, y trapezoide se basan en el área de un rectángulo. Las siguientes figuras muestran cómo cada uno de estos tres cuadriláteros se refiere a un rectángulo, y la siguiente lista te da los…
Identificar escaleno, isósceles y triángulos equiláteros Los triángulos se clasifican según la longitud de sus lados o la medida de sus ángulos. Estas clasificaciones vienen de tres en tres, al igual que los lados y ángulos de sí mismos.Las siguientes son las clasificaciones de triángulos basada en…
La identificación de triángulos por sus ángulos Se puede clasificar triángulos por sus ángulos, así como por sus lados. Las clasificaciones basadas en ángulos son como sigue:Triángulo aguda: Un triángulo con tres ángulos agudos (menos de 90 # 176-).Triángulo obtuso: Un triángulo con un…
Triángulos trigonométricas básicas Todo por su cuenta, los ángulos son sin duda muy emocionante. Pero los puso en un triángulo, y usted tiene la guinda del pastel. Triángulos son una de las figuras geométricas estudiadas con más frecuencia. Los ángulos que forman el triángulo…
Encuentre el área de un triángulo con asa Cuando se tienen dos ángulos en un triángulo y el lado entre ellos (ASA), puede utilizar trigonométrica para hallar el área del triángulo. Las fórmulas van como sigue.En el triángulo Abecedario, si las medidas de los lados son la, b, y c…
Cómo circunscribir un triángulo Cada triángulo puede ser circunscrito por un círculo, lo que significa que un círculo - y sólo uno - pasa por los tres vértices (esquinas) de cualquier triángulo. En términos de los laicos, cualquier triángulo puede encajar en algún…
¿Cómo encontrar el área de un triángulo con sas Cuando usted sabe las longitudes de dos de los lados de un triángulo más la medida del ángulo entre los lados (SAS), se encuentra el área del triángulo. Este método requiere un poco de trigonometría - usted tiene que encontrar el seno del…