Medición del volumen de una pirámide
Suponga que usted desea encontrar el volumen de una pirámide de base cuadrada de 6 x 6 unidades y una altura de 3 unidades. Geometría le dice que usted puede utilizar la siguiente fórmula:
Esta fórmula funciona muy bien, pero no te da una idea de cómo resolver problemas- similares funciona sólo para las pirámides. El método de carne máquina de cortar, sin embargo, proporciona un enfoque para el problema que se puede generalizar a utilizar para muchos otros tipos de sólidos.
Para empezar, te pincho esta pirámide en la X-eje de un gráfico, como se muestra en la figura. Observe que el vértice de la pirámide está en el origen, y el centro de la base está en el punto (3, 0).
Para encontrar el volumen exacto de la pirámide, esto es lo que hace:
Encuentra una expresión que representa el área de una sección transversal aleatoria de la pirámide en términos de X.
A X = 1, la sección transversal es 22 = 4. En X = 2, es 42 = 16. Y en X = 3, es 62 = 36. Así que en términos generales, el área de la sección transversal es:
LA = (2X)2 = 4X2
Utilice esta expresión para construir una integral definida que representa el volumen de la pirámide.
En este caso, los límites de integración son 0 y 3, por lo que:
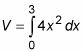
Evaluar esta integral:
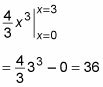
Esta es la misma respuesta proporcionado por la fórmula de la pirámide. Pero este método se puede aplicar a una variedad mucho más amplia de sólidos.
-
JavaFX: añadir un objeto de malla a un mundo 3D -
Conceptos de geometría a su estudiante de la escuela secundaria deben conocer las normas básicas comunes -
¿Cómo se mide en tres dimensiones -
Encontrar el volumen de un sólido con secciones transversales congruentes -
Encontrar el volumen de un sólido con secciones transversales similares -
Encontrar el volumen de un sólido utilizando el método de disco
¿Cómo funciona la integración: es sólo Además de lujo El significado más fundamental de la integración es sumar. Y cuando representas la integración en un gráfico, se puede ver el proceso de sumar como un resumen de finas tiras rectangulares de área para llegar al área total bajo la curva, como…
¿Cómo evaluar el volumen de un sólido de revolución Puede evaluar el volumen de un sólido de revolución. Un sólido de revolución se crea mediante la adopción de una función, o parte de una función, y girando alrededor de un eje - en la mayoría de los casos, ya sea la X-eje o la y-eje.Un…
¿Cómo encontrar el volumen de una forma circular con el método de la integración pila-de-panqueques Geometría te dice cómo calcular los volúmenes de sólidos sencillos. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas. La técnica de pila-de-panqueques funciona cuando las secciones…
¿Cómo encontrar el volumen de una forma complicada con el método de carne máquina de cortar de la integración En geometría, usted aprendió cómo calcular los volúmenes de sólidos simples como cajas, cilindros y esferas. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas.La metáfora de carne…
¿Cómo encontrar el volumen de una forma utilizando el método de la arandela de la integración Geometría te dice cómo calcular los volúmenes de sólidos sencillos. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas. Si usted tiene una forma circular con un agujero circular en el…
¿Cómo encontrar el volumen de un sólido entre dos superficies de revolución Si desea encontrar el volumen de un sólido que se encuentra entre dos superficies distintas de la revolución, puede utilizar el método de carne máquina de cortar para hacer esto. los Método de carne máquina de cortar funciona mejor con los…
Cómo medir el volumen de un sólido de forma irregular Se puede medir el volumen de cualquier sólido con una sección transversal que es una función de de forma irregular X. En algunos casos, estos sólidos son más difíciles de describir de lo que son para medir. Por ejemplo, echar un vistazo a esta…
¿Cómo medir el volumen de un objeto al convertirlo en su lado A veces, si se desea medir el volumen de un objeto, es necesario convertirla en su lado de modo que usted puede utilizar el método de carne máquina de cortar. Este método funciona mejor con los sólidos que tienen secciones transversales…
Cómo utilizar el método Shell para medir el volumen de un sólido los método de shell permite medir el volumen de un sólido mediante la medición del volumen de muchas superficies concéntricas de volumen, llamado " conchas ". Aunque el método de shell funciona sólo para sólidos con secciones transversales…
Presentaciones Textual en la prueba de ciencias ged Gran parte de la información científica presentada en el examen de GED Ciencia viene en forma de pasajes de lectura - uno o más párrafos de texto. El reto de estos pasajes es ser capaz de leer y entender el pasaje y tamizar a través de él para…
Fórmulas geométricas que usted debe saber para el examen de la base praxis Usted tendrá que saber fórmulas geométricas para el Examen Praxis Core. Las figuras geométricas tienen ciertas propiedades, y el número de dimensiones que tienen es parte de lo que decide qué otras propiedades que tienen. Los segmentos de…
Pirámide de alimento para los niños pequeños Se acabó la vieja pirámide de los alimentos que usted creció con, pero la nueva pirámide del Departamento de Agricultura de Estados Unidos (USDA) recomienda que se utiliza para planificar las comidas para los bebés y niños pequeños es un…