Cómo medir el volumen de un sólido de forma irregular
Se puede medir el volumen de cualquier sólido con una sección transversal que es una función de de forma irregular X. En algunos casos, estos sólidos son más difíciles de describir de lo que son para medir. Por ejemplo, echar un vistazo a esta cifra.
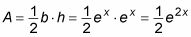
El sólido en la figura consiste en dos curvas exponenciales - que se describe por la ecuación y = eX y la otra describe mediante la colocación de la misma curva directamente en frente de la X-eje - unidos por líneas rectas. Los otros lados del sólido son planos acotados rebanar perpendicularmente en una variedad de direcciones.
Observe que cuando se mire esta sólida, perpendicular a la X-eje, su sección transversal es siempre un triángulo rectángulo isósceles. Esta es una forma fácil de medir, por lo que el método de corte funciona muy bien para medir el volumen de este sólido. Estos son los pasos:
Encuentra una expresión que representa el área de una sección transversal al azar del sólido.
El triángulo de la y-eje tiene una altura y la base de 1 - es decir, e0. Y el triángulo en la línea X = 1 tiene una altura y la base de e1, cual es e. En general, la altura y la base de cualquier sección transversal triangular es eX.
Así que aquí está cómo usar la fórmula del área de un triángulo para hallar el área de una sección transversal en términos de X:
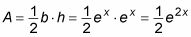
Utilice esta expresión para construir una integral definida que representa el volumen del sólido.
Ahora que ya sabe cómo medir el área de una sección transversal, integrar añadir todas las secciones transversales de X = 0 a X = 1:
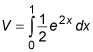
Evaluar esta integral para encontrar el volumen.
-
Intercepta y / o pendientes que cambian con el tiempo -
Encontrar el área de un triángulo utilizando sus coordenadas -
¿Cómo se mide en tres dimensiones -
¿Cómo medir los triángulos -
Encontrar el volumen de un sólido con secciones transversales congruentes -
Encontrar el volumen de un sólido con secciones transversales similares
Encontrar el volumen de un sólido utilizando el método de disco Cuando las secciones transversales de un sólido son todos los círculos, se puede dividir la forma en discos para encontrar su volumen. Así es como funciona. Digamos que usted necesita para encontrar el volumen de un sólido - entre X = 2 y X = 3…
¿Cómo funciona la integración: es sólo Además de lujo El significado más fundamental de la integración es sumar. Y cuando representas la integración en un gráfico, se puede ver el proceso de sumar como un resumen de finas tiras rectangulares de área para llegar al área total bajo la curva, como…
¿Cómo evaluar el volumen de un sólido de revolución Puede evaluar el volumen de un sólido de revolución. Un sólido de revolución se crea mediante la adopción de una función, o parte de una función, y girando alrededor de un eje - en la mayoría de los casos, ya sea la X-eje o la y-eje.Un…
¿Cómo encontrar el volumen de una forma circular con el método de la integración pila-de-panqueques Geometría te dice cómo calcular los volúmenes de sólidos sencillos. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas. La técnica de pila-de-panqueques funciona cuando las secciones…
¿Cómo encontrar el volumen de una forma complicada con el método de carne máquina de cortar de la integración En geometría, usted aprendió cómo calcular los volúmenes de sólidos simples como cajas, cilindros y esferas. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas.La metáfora de carne…
¿Cómo encontrar el volumen de una forma utilizando el método de la arandela de la integración Geometría te dice cómo calcular los volúmenes de sólidos sencillos. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas. Si usted tiene una forma circular con un agujero circular en el…
¿Cómo encontrar el volumen de una forma utilizando el método de la arandela Geometría te dice cómo calcular los volúmenes de sólidos sencillos. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas. Si usted tiene una forma redonda con un agujero en el centro, se…
¿Cómo encontrar el volumen de un sólido entre dos superficies de revolución Si desea encontrar el volumen de un sólido que se encuentra entre dos superficies distintas de la revolución, puede utilizar el método de carne máquina de cortar para hacer esto. los Método de carne máquina de cortar funciona mejor con los…
¿Cómo medir el volumen de un objeto al convertirlo en su lado A veces, si se desea medir el volumen de un objeto, es necesario convertirla en su lado de modo que usted puede utilizar el método de carne máquina de cortar. Este método funciona mejor con los sólidos que tienen secciones transversales…
Cómo utilizar el método Shell para medir el volumen de un sólido los método de shell permite medir el volumen de un sólido mediante la medición del volumen de muchas superficies concéntricas de volumen, llamado " conchas ". Aunque el método de shell funciona sólo para sólidos con secciones transversales…
Medición del volumen de una pirámide Suponga que usted desea encontrar el volumen de una pirámide de base cuadrada de 6 x 6 unidades y una altura de 3 unidades. Geometría le dice que usted puede utilizar la siguiente fórmula:Esta fórmula funciona muy bien, pero no te da una idea de…
Determinar el área de un triángulo desde su base y la altura Si conoce la base y la altura de un triángulo, puede utilizar una fórmula probada y verdadera para encontrar su área. Es probable que primero encontró con la fórmula básica área del triángulo en aproximadamente sexto o séptimo grado. Si ha…