Encontrar el volumen de un sólido utilizando el método de disco

categoría Educación y lenguas / Matemáticas / Cálculo

Cuando las secciones transversales de un sólido son todos los círculos, se puede dividir la forma en discos para encontrar su volumen. Así es como funciona. Digamos que usted necesita para encontrar el volumen de un sólido - entre X = 2 y X = 3 - generada por la rotación de la curva de y = eX acerca de X-eje (en la imagen).

Una pila de lado de los discos.
Una pila de lado de los discos.

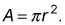
  1. Determinar el área de cualquier edad sección transversal.

    Cada sección transversal es un círculo con radio eX. Por lo tanto, su área viene dada por la fórmula para el área de un círculo,

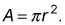
    image1.jpg

    Tapar eX dentro r te dio

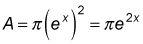
    image2.jpg

  2. Añadir dx para obtener el volumen de un disco representante infinitamente delgada.

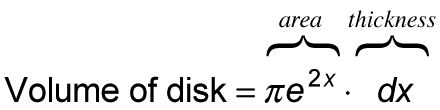
    image3.jpg

  3. Sume los volúmenes de los discos de 2 a 3 mediante la integración.

    image4.jpg

Un disco representativa se encuentra en ningún lugar en particular. Tenga en cuenta que el paso 1 se refiere a "cualquier edad" sección transversal. Se llama así porque cuando se tiene en cuenta un disco representativo como el que se muestra en la figura, usted debe centrarse en un disco que está en ningún lugar en particular. El que se muestra en la figura se encuentra a una desconocido posición en el X-eje, y su radio va desde el X-eje hasta la curva y = eX. Por lo tanto, su radio es la desconocido longitud de eX. Si, en cambio, se utiliza algún disco especial como la izquierda, más disco a X = 2, es más probable que cometa el error de pensar que un disco representante tiene alguna conocido radio como e2.



Artículos Relacionados

Sobre el autor
¿Cómo se mide en tres dimensiones ¿Cómo se mide en tres dimensiones

Medición en tres dimensiones es similar a la medición en dos dimensiones sin embargo, en 3-D, el límite de un sólido se llama su área de superficie (no su perímetro) Y lo que es el interior de un sólido se llama su volumen (no su área).El…

Encontrar el volumen de un sólido con secciones transversales congruentes Encontrar el volumen de un sólido con secciones transversales congruentes

Saber cómo se mide el volumen sin cálculo da sus frutos a lo grande cuando entras en la arena cálculo. Esto es estrictamente obviedad cosas - algunos geometría básica y sólida que usted probablemente ya sabe.Uno de los sólidos más simples…

Encontrar el volumen de un sólido con secciones transversales similares Encontrar el volumen de un sólido con secciones transversales similares

Encontrar el volumen de un prisma o cilindro es bastante sencillo. Pero lo que si usted necesita encontrar el volumen de una forma como la que se muestra aquí? En este caso, cortando paralelo a la base siempre resulta en la misma forma - un…

Encontrar volumen con el método de muñecas matryoshka (aka El método carcasa cilíndrica) Encontrar volumen con el método de muñecas matryoshka (aka El método carcasa cilíndrica)

Si usted ha estudiado algún cálculo integral, que sin duda ha de ejecutar a través de los métodos de disco y arandela para el volumen de cómputo: cortar un sólido en dados rodajas finas, cada uno la forma de un disco circular o arandela (un…

¿Cómo evaluar el volumen de un sólido de revolución ¿Cómo evaluar el volumen de un sólido de revolución

Puede evaluar el volumen de un sólido de revolución. Un sólido de revolución se crea mediante la adopción de una función, o parte de una función, y girando alrededor de un eje - en la mayoría de los casos, ya sea la X-eje o la y-eje.Un…

¿Cómo encontrar el volumen de una forma circular con el método de la integración pila-de-panqueques ¿Cómo encontrar el volumen de una forma circular con el método de la integración pila-de-panqueques

Geometría te dice cómo calcular los volúmenes de sólidos sencillos. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas. La técnica de pila-de-panqueques funciona cuando las secciones…

¿Cómo encontrar el volumen de una forma complicada con el método de carne máquina de cortar de la integración ¿Cómo encontrar el volumen de una forma complicada con el método de carne máquina de cortar de la integración

En geometría, usted aprendió cómo calcular los volúmenes de sólidos simples como cajas, cilindros y esferas. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas.La metáfora de carne…

¿Cómo encontrar el volumen de una forma cilíndrica con el método anidados-ruso-muñecas de la integración ¿Cómo encontrar el volumen de una forma cilíndrica con el método anidados-ruso-muñecas de la integración

Integración que permite calcular los volúmenes de una infinita variedad de formas complicadas que no se puede manejar con una geometría regular. Usted puede cortar un sólido en cilindros concéntricos delgadas y luego sumar los volúmenes de…

¿Cómo encontrar el volumen de una forma utilizando el método de la arandela de la integración ¿Cómo encontrar el volumen de una forma utilizando el método de la arandela de la integración

Geometría te dice cómo calcular los volúmenes de sólidos sencillos. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas. Si usted tiene una forma circular con un agujero circular en el…

¿Cómo encontrar el volumen de una forma utilizando el método de la arandela ¿Cómo encontrar el volumen de una forma utilizando el método de la arandela

Geometría te dice cómo calcular los volúmenes de sólidos sencillos. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas. Si usted tiene una forma redonda con un agujero en el centro, se…

¿Cómo encontrar el volumen de un sólido entre dos superficies de revolución ¿Cómo encontrar el volumen de un sólido entre dos superficies de revolución

Si desea encontrar el volumen de un sólido que se encuentra entre dos superficies distintas de la revolución, puede utilizar el método de carne máquina de cortar para hacer esto. los Método de carne máquina de cortar funciona mejor con los…

Cómo medir el volumen de un sólido de forma irregular Cómo medir el volumen de un sólido de forma irregular

Se puede medir el volumen de cualquier sólido con una sección transversal que es una función de de forma irregular X. En algunos casos, estos sólidos son más difíciles de describir de lo que son para medir. Por ejemplo, echar un vistazo a esta…

» » » » Encontrar el volumen de un sólido utilizando el método de disco