¿Cómo encontrar el volumen de una forma cilíndrica con el método anidados-ruso-muñecas de la integración

categoría Educación y lenguas / Matemáticas / Cálculo

Integración que permite calcular los volúmenes de una infinita variedad de formas complicadas que no se puede manejar con una geometría regular. Usted puede cortar un sólido en cilindros concéntricos delgadas y luego sumar los volúmenes de todos los cilindros. Es un poco como cómo esas muñecas rusas anidados encajan unas dentro de otras. O imaginar una lata de sopa que tiene de alguna manera muchas etiquetas de papel, cada una cubriendo el bajo ella. O imaginar una de esas ropas-linters de con los papeles pegajosos que despegarse. Cada sopa puede etiquetar o un pedazo de papel adhesivo es una carcasa cilíndrica - antes rompo, por supuesto. Después se desgarra si fuera poco, es un rectángulo normal.

Aquí hay un problema: Un sólido se genera mediante la adopción de la zona delimitada por la X-eje,

image0.jpg

y luego girándola sobre la y-eje. La siguiente figura muestra la idea. La zona gris claro es la forma que ha sido girado por la y-eje para crear todo el sólido 3-D.

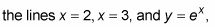
Una forma algo así como el Coliseo romano y una de sus conchas representativas.
Una forma algo así como el Coliseo romano y una de sus conchas representativas.

¿Cuál es el volumen?

  1. Determinar el área de una carcasa cilíndrica representativo.

    Cuando imaginando una cáscara representante, se centran en una cáscara que es en ningún lugar en particular. La figura muestra una concha como genérico. Su radio es desconocida, X, y su altura es la altura de la curva en X, a saber e a la potencia de X. Si, en cambio, se utiliza una concha especial como el más exterior cáscara con un radio de 3, es más probable que cometa el error de pensar que una cáscara representante tiene alguna conocido radio como 3 o una conocido altura como e a la potencia de 3. Tanto el radio y la altura son desconocido.

    Cada shell representante, al igual que la sopa se puede etiquetar o la hoja adhesiva de un de-linter, es sólo un rectángulo cuya área es, por supuesto, largo veces ancho.

    image2.jpg

    Así que ahora usted tiene la fórmula general para el área de un shell representante:

    image3.jpg

  2. Multiplique la zona por el grosor de la cáscara, dx, para obtener su volumen.

    image4.jpg

  3. Sume los volúmenes de todas las conchas de 2 a 3 mediante la integración.

    image5.jpg

Con cáscaras cilíndricas, no siempre está claro cuáles son los límites de la integración debe ser. Aquí tienes un consejo. A integrar desde el derecho borde del cilindro más pequeño hasta el derecho borde de un cilindro. Y tenga en cuenta que nunca se integra desde el borde izquierdo al borde derecho de los más grandes del cilindro (como -3-3).



Artículos Relacionados

Sobre el autor
Encontrar el volumen de un sólido utilizando el método de disco Encontrar el volumen de un sólido utilizando el método de disco

Cuando las secciones transversales de un sólido son todos los círculos, se puede dividir la forma en discos para encontrar su volumen. Así es como funciona. Digamos que usted necesita para encontrar el volumen de un sólido - entre X = 2 y X = 3…

¿Cómo funciona la integración: es sólo Además de lujo ¿Cómo funciona la integración: es sólo Además de lujo

El significado más fundamental de la integración es sumar. Y cuando representas la integración en un gráfico, se puede ver el proceso de sumar como un resumen de finas tiras rectangulares de área para llegar al área total bajo la curva, como…

¿Cómo evaluar el volumen de un sólido de revolución ¿Cómo evaluar el volumen de un sólido de revolución

Puede evaluar el volumen de un sólido de revolución. Un sólido de revolución se crea mediante la adopción de una función, o parte de una función, y girando alrededor de un eje - en la mayoría de los casos, ya sea la X-eje o la y-eje.Un…

¿Cómo encontrar el área entre dos curvas ¿Cómo encontrar el área entre dos curvas

Para encontrar el área entre dos curvas, lo que necesita para llegar a una expresión para un rectángulo estrecho que se encuentra en una curva y sube a otro.de X = 0 a X = 1:Para obtener la altura del rectángulo de representación en la figura,…

¿Cómo encontrar el volumen de una forma circular con el método de la integración pila-de-panqueques ¿Cómo encontrar el volumen de una forma circular con el método de la integración pila-de-panqueques

Geometría te dice cómo calcular los volúmenes de sólidos sencillos. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas. La técnica de pila-de-panqueques funciona cuando las secciones…

¿Cómo encontrar el volumen de una forma complicada con el método de carne máquina de cortar de la integración ¿Cómo encontrar el volumen de una forma complicada con el método de carne máquina de cortar de la integración

En geometría, usted aprendió cómo calcular los volúmenes de sólidos simples como cajas, cilindros y esferas. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas.La metáfora de carne…

¿Cómo encontrar el volumen de una forma utilizando el método de la arandela de la integración ¿Cómo encontrar el volumen de una forma utilizando el método de la arandela de la integración

Geometría te dice cómo calcular los volúmenes de sólidos sencillos. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas. Si usted tiene una forma circular con un agujero circular en el…

¿Cómo encontrar el volumen de una forma utilizando el método de la arandela ¿Cómo encontrar el volumen de una forma utilizando el método de la arandela

Geometría te dice cómo calcular los volúmenes de sólidos sencillos. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas. Si usted tiene una forma redonda con un agujero en el centro, se…

¿Cómo encontrar el volumen de un sólido entre dos superficies de revolución ¿Cómo encontrar el volumen de un sólido entre dos superficies de revolución

Si desea encontrar el volumen de un sólido que se encuentra entre dos superficies distintas de la revolución, puede utilizar el método de carne máquina de cortar para hacer esto. los Método de carne máquina de cortar funciona mejor con los…

Cómo utilizar el método Shell para medir el volumen de un sólido Cómo utilizar el método Shell para medir el volumen de un sólido

los método de shell permite medir el volumen de un sólido mediante la medición del volumen de muchas superficies concéntricas de volumen, llamado " conchas ". Aunque el método de shell funciona sólo para sólidos con secciones transversales…

Cómo calcular el área de un paralelogramo, cometa, o trapezoidal Cómo calcular el área de un paralelogramo, cometa, o trapezoidal

Las fórmulas del área para el paralelogramo, cometa, y trapezoide se basan en el área de un rectángulo. Las siguientes figuras muestran cómo cada uno de estos tres cuadriláteros se refiere a un rectángulo, y la siguiente lista te da los…

Fórmulas de geometría famosos que usted debe saber para el ASVAB Fórmulas de geometría famosos que usted debe saber para el ASVAB

Las subpruebas de matemáticas del ASVAB menudo piden que utilizar fórmulas básicas de geometría para calcular mediciones geométricas. Usted debe comprometerse estas fórmulas simples para la memoria si usted está esperando para una puntuación…

» » » » ¿Cómo encontrar el volumen de una forma cilíndrica con el método anidados-ruso-muñecas de la integración