Conceptos de geometría a su estudiante de la escuela secundaria deben conocer las normas básicas comunes
Para cumplir con las normas fundamentales comunes para las matemáticas, los estudiantes de secundaria deben estar familiarizados con algo de geometría. Geometría
es una rama de las matemáticas que estudia la naturaleza y propiedades de puntos, líneas, planos, y una multitud de formas, incluyendo rectángulos, triángulos, círculos y esferas.Congruencia
Los estudiantes muestran que dos figuras son congruente, lo que indica que todos los lados y ángulos de la forma son exactamente los mismos. Los estudiantes también utilizan movimientos rígidos para mover una forma sobre otra para demostrar que todas las partes son iguales. Movimientos rígidos implicar mover un objeto sin cambiar su tamaño o forma.
Echa un vistazo a el ejemplo de movimiento rígido (reflexión y la traducción en este caso) en el plano de coordenadas. Observe que el tamaño de la forma no ha cambiado a pesar de que se refleja hacia la izquierda y traducido abajo.
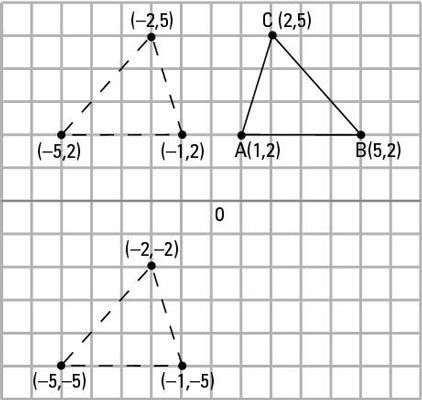
Círculos
Estándares Básicos Comunes requieren que al graduarse los estudiantes saben círculos dentro y por fuera. Las expectativas son las siguientes:
Explicar por qué todos los círculos son similares.
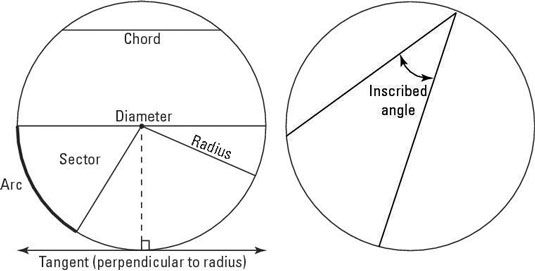
Dibuja ángulos inscritos, radios, tangentes y acordes y explicar cómo se relacionan.
Saber que el radio de un círculo es perpendicular a la tangente en el punto donde el radio toca el círculo.
Encuentra el área de cualquier propuesta sector de un círculo (imaginar un sector, imaginar una rebanada cortada de una pizza redonda).
Encuentra la longitud de un arco en el perímetro de un círculo (la longitud del lado curvado de un sector). (Los estudiantes de secundaria ya saben cómo encontrar la circunferencia - la longitud de todo el camino alrededor de un círculo.
Dibuja un círculo con un radio de seis pulgadas, con un sector que tiene un ángulo interior de 45 grados, y pídale a su hijo para calcular el área del sector. Tendrá que utilizar un compás y transportador para ser precisos con sus medidas.
La fórmula para el área de todo el círculo es A = # 960-r2 tan A = # 960- x 62 = 3.14159 x 32 = 100,53 pulgadas cuadradas. Un círculo es de 360 grados, por lo que el área del sector es 45/360 veces la superficie total del círculo. La fracción 45/360 reduce a 1/8, por lo que el área del sector es 100.53 x 01.08 = 12.57 redondeada a la centésima más cercana.
Utilizando el mismo círculo, pídale a su hijo para encontrar la longitud del arco del sector.
Para encontrar el arco, su hijo debe calcular la circunferencia del círculo y luego se multiplica por la misma fracción: 1/8. La fórmula para la circunferencia de un círculo es C = # 960-d dónde d es diámetro. El diámetro es dos veces el radio de 6 pulgadas o 12 pulgadas, por lo que C = # 960- x 12 = 37,70 redondeada a la centésima más cercana.
Así octavo de que está a punto 4.71.
Medición geométrica y la dimensión
Patrones de medida y dimensiones geométricas piden a los estudiantes a utilizar las fórmulas para los volúmenes de figuras tridimensionales, incluyendo esferas, conos, cilindros y pirámides:
Volumen de una esfera: 4/3 # 960-r2 donde r es el radio de la esfera
Volumen de un cono: Tercio # 960-r2h dónde r es el radio de la base del cono y h es su altura
Volumen de un cilindro: # 960-r2h dónde r es el radio de la base del cilindro y h es su altura
Volumen de una pirámide: 03.01bh dónde b es el área de la base de la pirámide y h es su altura
Pídale a su hijo para calcular el volumen de un cilindro que es 8 centímetros de altura y 10 centímetros de diámetro. Para resolver este problema, conecte los números en la fórmula para el volumen de un cilindro: # 960-r2h = # 960- x 102 x 8 = 3.14159 x 100 x 8 = 3.14159 x 800 = 2513.27 centímetros cúbicos.
Modelado geométrico
Modelado con llamadas de geometría en los estudiantes aplicar conceptos geométricos a situaciones del mundo real, tales como las siguientes:
Estimar el volumen de una piscina sobre el suelo utilizando la fórmula para el volumen de un cilindro.
Utilice fórmulas para el área y el volumen para calcular la densidad de población en un entorno determinado.
Diseñar una estructura utilizando varios métodos geométricos para lograr un objetivo específico, como el uso de la menor cantidad de materiales de construcción.
Haga que su hijo calcular el volumen o el espacio interior varios objetos tridimensionales o áreas alrededor de su casa. Por ejemplo, es posible que su hijo calcule el número de galones de agua de su calentador de agua contiene (sin mira a escondidas en el número en el calentador de agua, por supuesto).
Cómo determinar el área de sectores y segmentos de un círculo Marque una sección de un círculo con un arco y una cuerda, y usted tiene un segmento (este tipo de segmento tiene nada que ver con un segmento de línea). Lanzar un par de radios alrededor de un arco, y usted tiene un sector.Así que aquí están…
Cómo determinar la longitud de un arco La longitud de un arco significa la misma longitud que el sentido común siempre significa - usted sabe, al igual que la longitud de un trozo de cuerda (con un arco, por supuesto, sería una pieza curvada de cadena). Asegúrese de no mezclar hasta…
Ángulos en un círculo Hay varias maneras de dibujo un ángulo en un círculo, y cada uno tiene una forma especial de calcular el tamaño de ese ángulo. Cuatro tipos diferentes de ángulos son: central, inscrito, interior, y exterior. Aquí, verá ejemplos de estos…
Acordes frente tangentes de los círculos Usted muestra el diámetro y el radio de un círculo dibujando segmentos a partir de un punto en el círculo, ya sea hacia oa través del centro del círculo. Sin embargo, otras dos figuras rectas tienen un lugar en un círculo. Una de estas figuras…
Cómo localizar el centro de un círculo Una forma de describir el centro de un círculo es identificar la centroide. Este punto medio es el centro de gravedad, donde se puede equilibrar el triángulo y girar a su alrededor.Al graficar un círculo, triángulo, o segmento de línea mediante…
Cómo relacionarse radianes a exploraciones de radar La mayor ventaja de utilizar radianes en lugar de grados es que un radián está directamente relacionado con una longitud - la longitud o distancia alrededor de un círculo, que se llama su circunferencia. Usando radianes es muy útil cuando…
Cómo utilizar radianes para resolver un problema trig Usando radianes es muy útil cuando usted está haciendo aplicaciones de trigonometría que implican la longitud de un arco de un círculo, que es parte de su circunferencia. Esto podría incluir la medición de la barrida de una mano en un reloj o…
Radio, diámetro, circunferencia, y el área de círculos LA círculo es una figura geométrica que necesita sólo dos piezas que lo identifican y clasifican: su centro (o medio) y su radio (la distancia desde el centro hasta cualquier punto en el círculo). Después de elegir un punto para ser el centro…
Preparación ASVAB: revisión de geometría Usted tendrá que tener un conocimiento básico de la geometría para el ASVAB. Geometry es ". La rama de las matemáticas que se ocupa de la deducción de las propiedades, la medición, y las relaciones de puntos, líneas, ángulos y figuras en el…
Fórmulas de geometría famosos que usted debe saber para el ASVAB Las subpruebas de matemáticas del ASVAB menudo piden que utilizar fórmulas básicas de geometría para calcular mediciones geométricas. Usted debe comprometerse estas fórmulas simples para la memoria si usted está esperando para una puntuación…
¿Cómo resolver problemas geométricos en el ASVAB Problemas geométricos en el ASVAB requieren que calcular el volumen, perímetro, área, circunferencia, diámetro, y así sucesivamente de varias formas geométricas. Estos problemas no son muy difíciles con un poco de conocimiento de algunas…
Fórmulas geométricas que usted debe saber para el examen de la base praxis Usted tendrá que saber fórmulas geométricas para el Examen Praxis Core. Las figuras geométricas tienen ciertas propiedades, y el número de dimensiones que tienen es parte de lo que decide qué otras propiedades que tienen. Los segmentos de…