Preparación ASVAB: revisión de geometría

Usted tendrá que tener un conocimiento básico de la geometría para el ASVAB.

Geometry es ". La rama de las matemáticas que se ocupa de la deducción de las propiedades, la medición, y las relaciones de puntos, líneas, ángulos y figuras en el espacio a partir de sus condiciones definitorias por medio de ciertas propiedades asumidas de espacio " ¡Suena interesante!

Realmente, la geometría es simplemente la rama de las matemáticas que se ocupan de formas, líneas y ángulos. Desde la perspectiva de las subpruebas de matemáticas ASVAB, usted debería ser capaz de identificar formas geométricas básicas y conocer ciertas propiedades sobre ellos para que pueda determinar sus ángulos y medidas. Usted ve un montón de preguntas relacionadas con la geometría, tanto en el conocimiento de las matemáticas y de las subpruebas razonamiento aritmético del ASVAB.

Conozca todos los ángulos

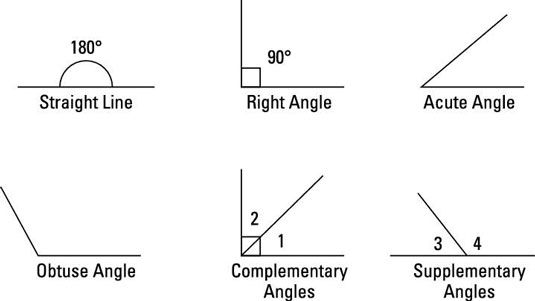
Ángulos se forman cuando dos líneas se cruzan en un punto. Muchas formas geométricas están formadas por líneas que se cruzan, que forman ángulos. Los ángulos se pueden medir en grados. Cuanto mayor es el número de grados, mayor será el ángulo es:

• Una línea recta es exactamente 180 # 176-.

• LA ángulo recto es exactamente 90 # 176-.

• Un ángulo agudo es más que 0 # 176- y menos de 90 # 176-.

• Un ángulo obtuso es más de 90 # 176- pero menos de 180 # 176-.

• Ángulos complementarios son dos ángulos que equivalen a 90 # 176- cuando se suman.

• Ángulos suplementarios son dos ángulos que igualan 180 # 176-Cuando se suman.

  

Formas geométricas comunes

Usted no necesita saber todas las formas geométricas para resolver los problemas de matemáticas que usted encuentra en el ASVAB. Sin embargo, debe reconocer las formas más comunes asociados con la geometría.

Conseguir plaza con cuadriláteros

LA cuadrilátero es una forma geométrica de cuatro lados. Todos los cuadriláteros contienen ángulos interiores suman 360 # 176-. Éstos son los cinco tipos más comunes de los cuadriláteros:

• Cuadrados tener cuatro lados de igual longitud, y todos los ángulos son ángulos rectos.

• Rectángulos tener todos los ángulos rectos.

• Rombos tener cuatro lados de igual longitud, pero los ángulos no tienen que ser ángulos rectos.

• Trapecios tener al menos dos lados que son paralelos.

• Paralelogramos tener lados opuestos que son paralelos, y sus lados y ángulos opuestos son iguales.

  

Probar triángulos

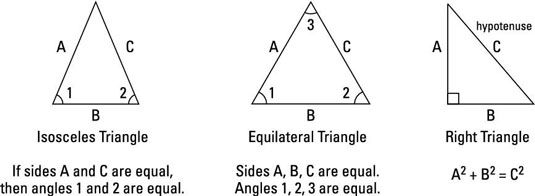
LA triángulo consta de tres líneas rectas cuyos tres ángulos internos siempre suman 180 # 176-. Los lados de un triángulo se denominan piernas. Los triángulos se pueden clasificar de acuerdo con la relación entre sus ángulos, la relación entre sus lados, o alguna combinación de estas relaciones. Usted debe conocer los tres tipos más comunes de triángulos:

• Triángulo isósceles: Tiene dos lados iguales y los ángulos opuestos a los lados iguales también son iguales.

• Triángulo equilátero: Tiene tres lados iguales y todos los ángulos miden 60 # 176-.

• Triángulo rectángulo: Tiene un ángulo recto (90 # 176 -) -, por lo tanto, los dos ángulos restantes son complementario (añadir hasta 90 # 176-). El lado opuesto al ángulo recto se llama hipotenusa, que es el lado más largo de un triángulo rectángulo.

  

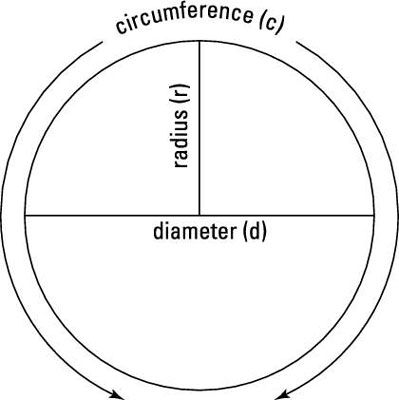
Instalarse en círculos

LA círculo se forma cuando los puntos de una línea cerrada están situados a distancias iguales desde un punto llamado centro del círculo. Un círculo siempre tiene 360 ​​# 176-. La línea cerrada de un círculo se llama su perímetro o circunferencia.

los radio de un círculo es la medida desde el centro del círculo a cualquier punto de la circunferencia del círculo. los diámetro del círculo se mide como una línea que pasa a través del centro del círculo, desde un punto en un lado del círculo hasta un punto en el otro lado del círculo. El diámetro de un círculo es siempre el doble de largo que el radio.