Matemáticas normas fundamentales comunes: propiedades geométricas como ecuaciones
Los estudiantes utilizan lo que saben acerca de las operaciones de álgebra para demostrar (o probar) ciertos aspectos o características de formas geométricas de las normas fundamentales comunes. Por ejemplo, si usted sabe que los tres ángulos interiores de un triángulo tienen que suman 180 grados y que los primeros dos ángulos son de 70 y 50 grados, usted sabe que el tercer ángulo es de 180 - 70 - 50 = 60 grados.
Los estudiantes también empiezan a explorar secciones cónicas (o simplemente cónicas) - Curvas, círculos o elipses formadas por un corte en lonchas plano a través de un cono.
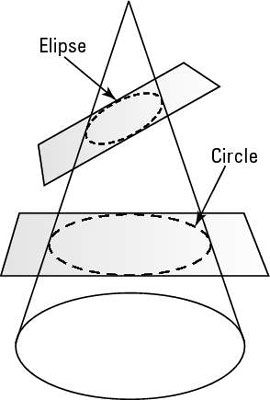
Al graduarse, los estudiantes deben ser capaces de traducir entre la ecuación y la representación gráfica de las secciones cónicas.
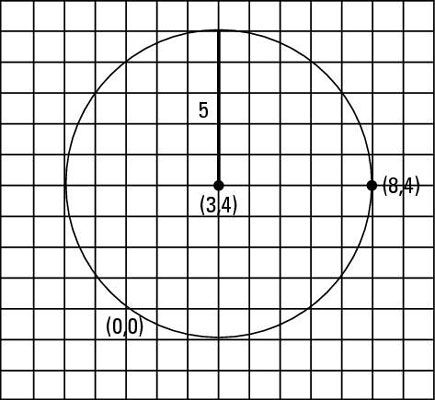
Si el centro de un círculo se representa por (h, k) Como un par ordenado, entonces la ecuación de un círculo es (X - h) 2 + (y - k) 2 = r2, con r siendo el radio. Para nuestros propósitos, digamos que el centro del círculo está en (3, 4) y que el radio del círculo es 5.
Si graficas esto en un plano de coordenadas, entonces todos los puntos que se encuentran en la circunferencia del círculo pueden sustituir a los valores de X y y en la ecuación.
Para probar si usted ha graficaste el círculo correctamente, seleccione un punto que usted sabe debe estar en la circunferencia y la inserta en la ecuación. Por ejemplo, el par ordenado (8, 4) debe estar en la circunferencia. Cuando sustituyes (8, 4) para X y y, la ecuación sigue siendo cierto.
(8 - 3) 2 + (4 - 4) 2 = 25
52 = 25
La ecuación representa una sección transversal de un cono tomada paralela a la base. La ecuación define un círculo con un centro en X = 3, y = 4 y un radio de 5.
-
Construir círculos en jr Cabri. En la TI-84 Plus -
Conceptos de geometría a su estudiante de la escuela secundaria deben conocer las normas básicas comunes -
Las secciones cónicas en pre-cálculo -
¿Cómo encontrar la ecuación de asíntotas -
Cómo graficar un círculo -
Cómo graficar las secciones cónicas en forma paramétrica
2 maneras de graficar un círculo Círculos son fáciles de trabajar en pre-cálculo. Un círculo tiene un centro, un radio, y un montón de puntos, pero sigue pasos ligeramente diferentes, dependiendo de si está mostrando el gráfico de un círculo centrado en el origen o desde el…
Cómo graficar las secciones cónicas en forma polar basado en la excentricidad Al graficar las secciones cónicas en el plano polar, utiliza ecuaciones que dependen de un valor especial conocido como excentricidad, que describe la forma general de una sección cónica. El valor de la excentricidad de una cónica puede decirle…
Cómo identificar las cuatro secciones cónicas en forma de ecuación Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…
Cómo identificar las cuatro secciones cónicas en forma de gráfico Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…
Cómo medir ángulos con radianes Grados no son la única forma de medir los ángulos. También puede utilizar radianes. Grados y radianes son sólo dos formas diferentes de medir ángulos, como pulgadas y centímetros son dos formas de medir la longitud.los radián medida de un…
Cómo trazar los grandes ángulos de todo el círculo unidad Usted puede tomar los ángulos unidad de círculo y los triángulos rectángulos especiales y ponerlos juntos para crear un pequeño paquete: el círculo unidad completa. Usted crea triángulos especiales en el círculo unidad uno a la vez, porque…
Definir el radián en la trigonometría Introducción de una persona para ángulos es por lo general en términos de grados. Es probable que tenga una buena idea de lo que es un ángulo de 45 grados se parece. E incluso la mayoría de los estudiantes de secundaria saben que un triángulo…
Cómo calcular las coordenadas en el origen de cualquier círculo unidad Usted no necesita un círculo unidad a utilizar esta coordenada negocio al determinar los valores de la función de los ángulos graficadas en posición estándar en un círculo. Puede utilizar un círculo con cualquier radio, siempre y cuando el…
Cómo calcular funciones trigonométricas usando cualquier círculo Cuando la determinación de los valores de la función trigonométrica de ángulos graficadas en la posición estándar en un círculo cuyo centro está en el origen, usted no tiene que tener un círculo unitario para calcular coordenadas. Puede…
Cómo calcular las funciones trigonométricas de ángulos usando el círculo unitario Cálculo de funciones trigonométricas de ángulos dentro de un círculo unidad es muy fácil. La figura muestra un círculo unitario, que tiene la ecuación X2 + y2 = 1, junto con algunos puntos de la circunferencia y sus coordenadas.El uso de los…
Cómo circunscribir un triángulo Cada triángulo puede ser circunscrito por un círculo, lo que significa que un círculo - y sólo uno - pasa por los tres vértices (esquinas) de cualquier triángulo. En términos de los laicos, cualquier triángulo puede encajar en algún…
Cómo hacer puntos en un círculo unitario los círculo unitario es un círculo con su centro en el origen del plano de coordenadas y con un radio de 1 unidad. Cualquier círculo con su centro en el origen tiene la ecuación X2 + y2 = r2, dónde r es el radio del círculo. En el caso de un…