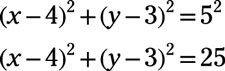Las secciones cónicas en pre-cálculo
Las secciones cónicas puede ser descrito o ilustrado con exactamente lo que su nombre indica: conos. Imagina un cono anaranjado en la calle, que dirigir en la dirección correcta. Entonces imaginar algún ingeniero de caminos inteligente colocar un cono en la parte superior de la otra, de punta a punta. Ese ingeniero está tratando de demostrar cómo se puede crear secciones cónicas.
Si usted viene a lo largo y cortar uno de esos conos paralelo al suelo, los bordes de corte forman un círculo. Cortar el cono en un ángulo, y usted tiene una elipse. Cortar el cono paralelo a uno de los lados, y usted tiene una parábola. Y, por último, cortar a través de los dos conos juntos, perpendicular al suelo, y usted tiene una hipérbola.
Si estas descripciones no funcionan para usted, los problemas de la práctica debe hacer el truco.
Usted va a trabajar en las secciones cónicas en las siguientes maneras:
Reconociendo que cónicas que se tiene de la ecuación general
Encontrar a los centros de los círculos y elipses
La determinación de los focos de círculos, elipses, y parábolas
El uso de la directriz de una parábola para completar el esbozo
Escribir las ecuaciones de las asíntotas de una hipérbola
Cambio de las ecuaciones básicas de sección cónica de paramétrico para rectangular
Cuando se trabaja con secciones cónicas, algunos desafíos incluirán lo siguiente:
La determinación del eje mayor de una elipse
Trazar la gráfica de una parábola en la dirección correcta
El uso de las asíntotas de una hipérbola correctamente en un gráfico
Encontrar a la raíz cuadrada de la ecuación de un círculo al encontrar el radio
Problemas de práctica
Nombra la cónica y su centro.
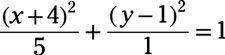
Responder: centro ellipse-: (-4, 1)
La forma estándar de la ecuación de una elipse con centro en (h, k) es
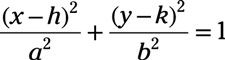
La ecuación dada ya está en esta forma, para que pueda identificar el centro coordina examinado los valores sustituidos por h y k.
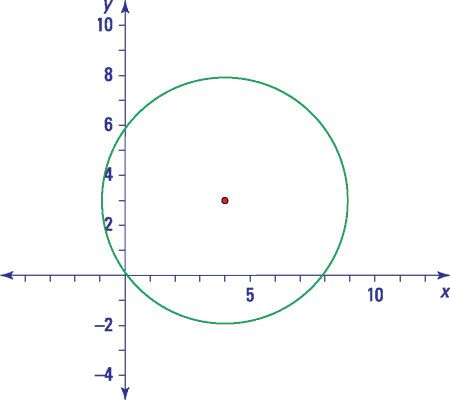
Escribe la ecuación del círculo descrito. Luego grafica el círculo: Centro: (4, 3) - radio: 5
Responder: (X - 4)2 + (y - 3)2 = 25
La ecuación estándar de un círculo con radio (h, k) Y el radio r es (X -h)2 + (y - k)2 = r2. Sustituir el punto dado (4, 3) para el (h, k) Y la cuadratura del 5:
-
Dibuja círculos y tangentes en una TI-83 Plus gráfico -
Matemáticas normas fundamentales comunes: propiedades geométricas como ecuaciones -
Curvas Crossing: encontrar las intersecciones de parábolas y círculos -
Descubriendo ecuaciones cónicas (accidentalmente) -
Encontrar las intersecciones de las líneas y las parábolas - Completando el cuadrado para las secciones cónicas
Encontrar las piezas clave de todas las hipérbolas LA hipérbola es el conjunto de todos los puntos en el plano de tal manera que la diferencia de las distancias a dos puntos fijos (la focos) Es una constante positiva. Hipérbolas siempre vienen en dos partes, y cada uno es un espejo perfecto…
¿Cómo encontrar la ecuación de asíntotas En pre-cálculo, puede que tenga que encontrar la ecuación de asíntotas para ayudarle a esbozar las curvas de una hipérbola. Debido a hipérbolas están formados por una curva donde la diferencia de las distancias entre dos puntos es constante,…
Cómo graficar un círculo La primera cosa que hay que saber para graficar la ecuación de un círculo es donde en un plano se encuentra el centro. La ecuación de un círculo aparece comoEsto se llama el centro-radio forma (o formulario estándar), ya que le da dos piezas de…
Cálculo: cómo representar gráficamente una elipse Una elipse es básicamente un círculo que ha sido aplastado, ya sea horizontal o verticalmente. Desde una perspectiva de pre-cálculo, un elipse es un conjunto de puntos en un plano, la creación de un óvalo, forma curvada de tal manera que la…
Cómo representar gráficamente una parábola vertical, Con el fin de representar gráficamente una parábola correctamente, es importante tener en cuenta si es una horizontal o una parábola vertical. Esto es porque mientras que las variables y constantes en las ecuaciones para las dos curvas tienen el…
Cómo graficar una elipse Un elipse es un conjunto de puntos en un plano, la creación de un óvalo, forma curvada, de tal manera que la suma de las distancias desde cualquier punto de la curva a dos puntos fijos (la focos) Es una constante (siempre la misma). Una elipse es…
Cómo graficar las secciones cónicas en forma paramétrica A veces, su profesor de pre-cálculo puede pedirle que gráfico de una cónica en forma paramétrica. Forma paramétrica es una forma elegante de decir una forma en la que usted puede hacer frente a las cónicas que no se expresan fácilmente como…
2 maneras de graficar un círculo Círculos son fáciles de trabajar en pre-cálculo. Un círculo tiene un centro, un radio, y un montón de puntos, pero sigue pasos ligeramente diferentes, dependiendo de si está mostrando el gráfico de un círculo centrado en el origen o desde el…
Cómo graficar las secciones cónicas en forma polar basado en la excentricidad Al graficar las secciones cónicas en el plano polar, utiliza ecuaciones que dependen de un valor especial conocido como excentricidad, que describe la forma general de una sección cónica. El valor de la excentricidad de una cónica puede decirle…
Cómo identificar las cuatro secciones cónicas en forma de ecuación Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…
Cómo identificar las cuatro secciones cónicas en forma de gráfico Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…
¿Cómo resolver sistemas no lineales En un sistema no lineal, al menos una ecuación tiene una gráfica que no es una línea recta - es decir, al menos una de las ecuaciones tiene que ser no lineal. Su instructor de pre-cálculo le dirá que siempre se puede escribir una ecuación…