Cómo graficar una elipse
Un elipse es un conjunto de puntos en un plano, la creación de un óvalo, forma curvada, de tal manera que la suma de las distancias desde cualquier punto de la curva a dos puntos fijos (la focos) Es una constante (siempre la misma). Una elipse es básicamente un círculo que ha sido aplastado, ya sea horizontal o verticalmente.
Gráficamente hablando, es necesario conocer dos tipos diferentes de elipses: horizontal y vertical. Una elipse horizontal es corta y grasa una vertical es alto y flaco. Cada tipo de elipse tiene las siguientes partes principales:
El punto en el centro de la elipse se llama centro y es nombrado (h, v) Al igual que el vértice de una parábola y el centro de un círculo.
los eje mayor es la línea que pasa por el centro de la elipse el camino más largo. La variable la es la letra usado para nombrar la distancia desde el centro de la elipse en el eje mayor. Los puntos finales del eje mayor de la elipse son y se llaman vértices.
los eje menor es perpendicular al eje mayor y se ejecuta a través del centro de la forma corta. La variable b es la letra usada para nombrar la distancia a la elipse del centro en el eje menor. Debido a que el eje mayor es siempre más largo que el menor de edad, la > b. Los criterios de valoración en el eje de menor importancia son llamados compañeros de vértices.
los focos son los dos puntos que dictan la cantidad de grasa o cómo flaca la elipse es. Siempre se encuentran en el eje mayor, y se pueden encontrar por la siguiente ecuación:
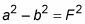
dónde la y b se mencionan como en las viñetas anteriores, y F es la distancia desde el centro hacia cada foco.
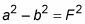
Esta figura muestra una elipse horizontal y una elipse vertical con sus partes etiquetadas. Observe que la longitud del eje mayor es 2la, y la longitud del eje menor es 2b. Esta figura también muestra la colocación correcta de los focos - siempre en el eje mayor.
Dos tipos de ecuaciones se aplican a elipses, dependiendo de si son horizontal o vertical:
La ecuación horizontal es
con el centro en (h, v), Eje mayor de 2la, y eje menor de 2b.
La ecuación vertical es
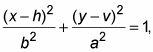
con las mismas partes - aunque la y b tienen lugares conmutadas.
Cuando el número más grande la está debajo X, la elipse es horizontal- cuando el número más grande es bajo y, es vertical.
Tienes que estar preparado para no sólo elipses gráfico, sino también para nombrar todas sus partes. Si un problema te pide que calcular las partes de una elipse, usted tiene que estar preparado para hacer frente a algunas raíces y / o decimales cuadrados feas. A continuación se presenta las partes de ambas elipses horizontales y verticales.
Elipse Horizontal
Centro: (h, v)
Vértices: (h # 177- la, v)
Compañeros de vértices: (h, v # 177- b)
Longitud del eje principal: 2la
Longitud del eje menor: 2b
Vertical Elipse
Centro: (h, v)
Vértices: (h, v # 177- la)
Compañeros de vértices: (h # 177- b, v)
Longitud del eje principal: 2la
Longitud del eje menor: 2b
Para encontrar los vértices de una elipse horizontal, utilice (h # 177- la, v) - Para encontrar los compañeros de vértices, utilice (h, v # 177- b). Una elipse vertical tiene vértices en (h, v # 177- la) Y compañeros de vértices en (h # 177- b, v).
Por ejemplo, mira
que ya está en la forma adecuada para graficar. Tu sabes h = 5 y v = -1 (Conmutación de las señales dentro de los paréntesis).
Este ejemplo es una elipse vertical porque el número más grande es bajo y, así que asegúrese de usar la fórmula correcta. Esta ecuación tiene vértices en (5, -1 # 177- 4), o (5, 3) y (5, -5). Tiene compañeros de vértices en (5 # 177- 3, -1), o (8, -1) y (2, -1).
El eje mayor en una elipse horizontal viene dado por la ecuación y = v- el eje menor está dada por X = h. El eje mayor en una elipse vertical está representado por X = h- el eje menor está representado por y = v. La longitud del eje mayor es 2la, y la longitud del eje menor es 2b.
Se puede calcular la distancia desde el centro a los focos en una elipse (ya sea la variedad) mediante el uso de la ecuación
dónde F es la distancia desde el centro hacia cada foco. Los focos siempre aparece en el eje mayor en la distancia dada (F) del centro.
¿Qué pasa si la ecuación elíptica que te dan no está en forma estándar? Echa un vistazo a el ejemplo
Siga estos pasos para poner la ecuación en la forma estándar:
Añadir la constante hacia el otro lado.
Esto le da
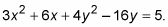
Completar el cuadrado.
Usted necesita factorizar dos constantes diferentes ahora - los diferentes coeficientes para
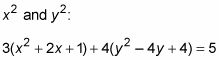
Equilibrar la ecuación mediante la adición de los nuevos términos para el otro lado.
En otras palabras,
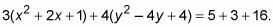
Nota: Adición de 1 y 4 dentro de los paréntesis realmente significa añadir
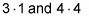
a cada lado, porque se debe multiplicar por el coeficiente antes de añadir a la derecha.
Factor el lado izquierdo de la ecuación y simplificar derecha.
Ahora tiene
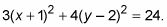
Divida la ecuación por la constante en el derecho a obtener 1 y luego reducir las fracciones.
Ahora tiene la forma
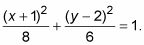
Determinar si la elipse es horizontal o vertical.
Debido a que el número más grande es bajo X, esta elipse es horizontal.
Encontrar el centro y la longitud de los ejes mayor y menor.
El centro está ubicado en (h, v), O (-1, 2).
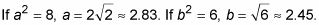
Grafica la elipse para determinar los vértices y compañeros de vértices.
Ir al centro de la primera y marcar el punto.
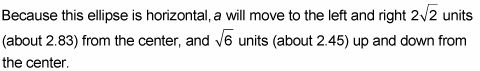
Trazado de estos puntos localizará los vértices de la elipse.
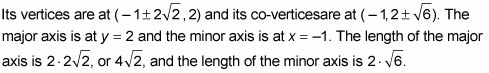
Trazar los focos de la elipse.
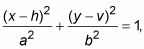
Usted determina la distancia focal desde el centro hacia los focos en esta elipse con la ecuación
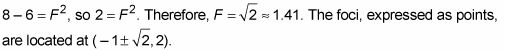
La figura anterior muestra todas las partes de esta elipse en su gloria grasa.
Las secciones cónicas en pre-cálculo Las secciones cónicas puede ser descrito o ilustrado con exactamente lo que su nombre indica: conos. Imagina un cono anaranjado en la calle, que dirigir en la dirección correcta. Entonces imaginar algún ingeniero de caminos inteligente colocar un…
Encontrar las piezas clave de todas las hipérbolas LA hipérbola es el conjunto de todos los puntos en el plano de tal manera que la diferencia de las distancias a dos puntos fijos (la focos) Es una constante positiva. Hipérbolas siempre vienen en dos partes, y cada uno es un espejo perfecto…
Cómo graficar un círculo La primera cosa que hay que saber para graficar la ecuación de un círculo es donde en un plano se encuentra el centro. La ecuación de un círculo aparece comoEsto se llama el centro-radio forma (o formulario estándar), ya que le da dos piezas de…
Cómo representar gráficamente una parábola horizontal Una parábola horizontal cuenta con sus propias ecuaciones para encontrar su partes- estos son sólo un poco diferente en comparación con una parábola vertical. La distancia al foco y la directriz desde el vértice en este caso es horizontal,…
Cómo graficar una hipérbola en 5 pasos Al graficar una hipérbola, se puede pensar que es una mezcla de dos parábolas - cada uno de ellos una imagen de espejo perfecto de la otra, y cada apertura de distancia el uno del otro. La definición matemática de una hipérbola es el conjunto…
Cómo graficar una hipérbola Piense de una hipérbola como una mezcla de dos parábolas - cada una de ellas una imagen de espejo perfecto de la otra, cada abertura de distancia el uno del otro. Los vértices de estos parábolas están a una distancia dada de separación, y se…
Cálculo: cómo representar gráficamente una elipse Una elipse es básicamente un círculo que ha sido aplastado, ya sea horizontal o verticalmente. Desde una perspectiva de pre-cálculo, un elipse es un conjunto de puntos en un plano, la creación de un óvalo, forma curvada de tal manera que la…
Cómo representar gráficamente una parábola vertical, Con el fin de representar gráficamente una parábola correctamente, es importante tener en cuenta si es una horizontal o una parábola vertical. Esto es porque mientras que las variables y constantes en las ecuaciones para las dos curvas tienen el…
2 maneras de graficar un círculo Círculos son fáciles de trabajar en pre-cálculo. Un círculo tiene un centro, un radio, y un montón de puntos, pero sigue pasos ligeramente diferentes, dependiendo de si está mostrando el gráfico de un círculo centrado en el origen o desde el…
Cómo graficar las secciones cónicas en forma polar basado en la excentricidad Al graficar las secciones cónicas en el plano polar, utiliza ecuaciones que dependen de un valor especial conocido como excentricidad, que describe la forma general de una sección cónica. El valor de la excentricidad de una cónica puede decirle…
Cómo identificar las cuatro secciones cónicas en forma de ecuación Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…
Cómo identificar las cuatro secciones cónicas en forma de gráfico Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…