Cómo graficar una hipérbola en 5 pasos
Al graficar una hipérbola, se puede pensar que es una mezcla de dos parábolas - cada uno de ellos una imagen de espejo perfecto de la otra, y cada apertura de distancia el uno del otro. La definición matemática de una hipérbola es el conjunto de todos los puntos en los que la diferencia en la distancia entre dos puntos fijos (llamado focos) Es constante. Hipérbolas vienen en dos tipos: horizontales y verticales.
Un horizontal y una hipérbola vertical, diseccionado para su placer visual.
La ecuación para una hipérbola horizontal es
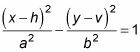
La ecuación para una hipérbola vertical es
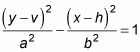
Para graficar una hipérbola, como este ejemplo,
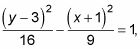
usted sigue estos sencillos pasos:
Marque el centro.
Debido a que esta ecuación es una hipérbola vertical, te encuentras con que el centro (h, v) De esta hipérbola es (-1, 3). Recuerde, los signos de los números dentro de los paréntesis son opuestas a las de las coordenadas del centro. Asimismo, recuerda que h está dentro de los paréntesis con X, y v está dentro de los paréntesis con y. Para este ejemplo, la cantidad con y cuadrado es lo primero, pero h y v no cambiar de lugar. los h y v siendo siempre fiel a sus respectivas variables, X y y.
Desde el centro en el paso 1, encontrar la transversal y ejes conjugados.
Ir arriba y abajo del eje transversal a una distancia de 4 (porque 42 está debajo y) Y, a continuación, ir a la derecha y la izquierda 3 (porque 32 está debajo X). Pero no conectar los puntos para obtener una elipse! Hasta ahora, los pasos de la elaboración de una hipérbola eran exactamente los mismos que para dibujar una elipse, pero aquí es donde las cosas se ponen diferentes: Los puntos que ha marcado como la (en el eje transversal) son sus vértices.
Utiliza estos puntos para dibujar un rectángulo que ayudará a guiar la forma de su hipérbola.
Porque te fuiste y abajo 4, la altura del rectángulo es 8- ir a la izquierda y la derecha 3 le da una anchura de 6.
Dibujar líneas diagonales a través del centro y las esquinas del rectángulo que se extienden más allá del rectángulo.
Este paso le da dos líneas que serán sus asíntotas.
Dibuje las curvas.
Comenzando en cada vértice por separado, dibujar las curvas que se aproximan a las asíntotas cuanto más lejos de los vértices de la curva recibe. La gráfica se acerca a las asíntotas, pero en realidad nunca los toca.
Creación de un rectángulo para representar gráficamente una hipérbola con asíntotas.
Esta figura muestra la hipérbola terminado.
Sobre el autor
 Cómo representar gráficamente una parábola horizontal
Cómo representar gráficamente una parábola horizontal Una parábola horizontal cuenta con sus propias ecuaciones para encontrar su partes- estos son sólo un poco diferente en comparación con una parábola vertical. La distancia al foco y la directriz desde el vértice en este caso es horizontal,…
 Cómo graficar una hipérbola
Cómo graficar una hipérbola Piense de una hipérbola como una mezcla de dos parábolas - cada una de ellas una imagen de espejo perfecto de la otra, cada abertura de distancia el uno del otro. Los vértices de estos parábolas están a una distancia dada de separación, y se…
 Cálculo: cómo representar gráficamente una elipse
Cálculo: cómo representar gráficamente una elipse Una elipse es básicamente un círculo que ha sido aplastado, ya sea horizontal o verticalmente. Desde una perspectiva de pre-cálculo, un elipse es un conjunto de puntos en un plano, la creación de un óvalo, forma curvada de tal manera que la…
 Cómo graficar una función racional con denominador que tiene el grado más alto
Cómo graficar una función racional con denominador que tiene el grado más alto Después de calcular todas las asíntotas y la X- y y-intercepciones para una función racional, que tienen toda la información que necesita para empezar a graficar la función. En cualquier función racional donde el denominador tiene un grado…
 Cómo representar gráficamente una parábola vertical,
Cómo representar gráficamente una parábola vertical, Con el fin de representar gráficamente una parábola correctamente, es importante tener en cuenta si es una horizontal o una parábola vertical. Esto es porque mientras que las variables y constantes en las ecuaciones para las dos curvas tienen el…
 Cómo graficar una elipse
Cómo graficar una elipse Un elipse es un conjunto de puntos en un plano, la creación de un óvalo, forma curvada, de tal manera que la suma de las distancias desde cualquier punto de la curva a dos puntos fijos (la focos) Es una constante (siempre la misma). Una elipse es…
 2 maneras de graficar un círculo
2 maneras de graficar un círculo Círculos son fáciles de trabajar en pre-cálculo. Un círculo tiene un centro, un radio, y un montón de puntos, pero sigue pasos ligeramente diferentes, dependiendo de si está mostrando el gráfico de un círculo centrado en el origen o desde el…
 Cómo graficar las secciones cónicas en forma polar basado en la excentricidad
Cómo graficar las secciones cónicas en forma polar basado en la excentricidad Al graficar las secciones cónicas en el plano polar, utiliza ecuaciones que dependen de un valor especial conocido como excentricidad, que describe la forma general de una sección cónica. El valor de la excentricidad de una cónica puede decirle…
 Cómo identificar las cuatro secciones cónicas en forma de ecuación
Cómo identificar las cuatro secciones cónicas en forma de ecuación Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…
 Cómo identificar las cuatro secciones cónicas en forma de gráfico
Cómo identificar las cuatro secciones cónicas en forma de gráfico Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…
 ¿Cómo trabajar con líneas en el cálculo
¿Cómo trabajar con líneas en el cálculo Una línea es la función más simple que se puede representar gráficamente en el plano de coordenadas. (Líneas son importantes en el cálculo porque cuando te acercas lo suficiente en una curva, se ve y se comporta como una línea.) Esta figura…
 Libro Pre-cálculo para dummies
Libro Pre-cálculo para dummies Logaritmos son simplemente otra manera de escribir exponentes. Las funciones exponenciales y logarítmicas son inversas entre sí. Para resolver y graficar funciones logarítmicas (logs), recuerde esta relación inversa y podrás registros resolver…
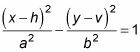
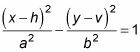
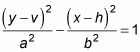
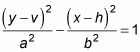 Creación de un rectángulo para representar gráficamente una hipérbola con asíntotas.
Creación de un rectángulo para representar gráficamente una hipérbola con asíntotas.





