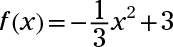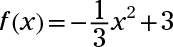La gráfica de una función cuadrática es una superficie lisa, U
-curva en forma que se abre hacia arriba o hacia abajo, dependiendo del signo del coeficiente de la
X2 término. El vértice e intercepta ofrecen los puntos más fáciles, más rápidas para ayudar con la gráfica de la parábola.
Puede recurrir a la solución de otros puntos si la gráfica no tiene X-intercepta o si necesita información adicional para determinar más acerca de la forma.
Otra ayuda para utilizar cuando graficar parábolas es el eje de Simetría una parábola es simétrica alrededor de una línea vertical que pasa por el vértice. Puntos a cada lado del eje de simetría que tienen el mismo y-valor son la misma distancia del eje. La ecuación de la eje de simetría es X = h, dónde (h, k) Es el vértice de la parábola.
Ejemplo de pregunta
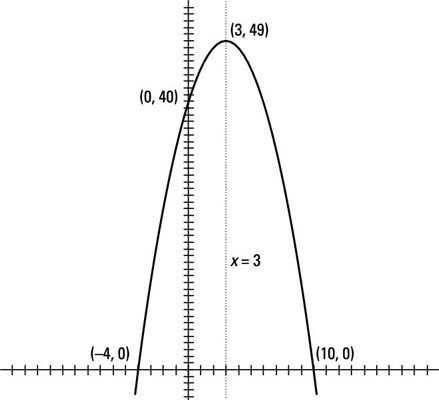
Dibuje la gráfica de la parábola F(X) = -X2 + 6X + 40, marcar ninguno intercepta y el vértice y que muestra el eje de simetría.
Como se puede ver, el y-intersección es (0, 40) - se puede encontrar al dejar todo el XEs por igual a 0 y la simplificación. Encuentra el X-intercepta mediante el establecimiento -X2 + 6X + 40 igual a 0 y la factorización: 0 = - (X2 - 6X - 40) = - (X + 4) (X - 10) - X = -4 Y 10, por lo que las intersecciones están en (-4, 0) y (10, 0).
El vértice está en (3, 49): Usted encuentra el X-valor y luego reemplazar el X's con 3s y simplificar para el y-de coordenadas.
Preguntas de práctica
Dibuje la gráfica de la parábola F(X) = 4X2, marcar ninguno intercepta y el vértice y que muestra el eje de simetría.
Dibuje la gráfica de la parábola
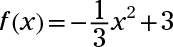
marcar ninguno intercepta y el vértice y que muestra el eje de simetría.
Dibuje la gráfica de la parábola F(X) = 3X2 - 6X - 9, marcar ninguno intercepta y el vértice y que muestra el eje de simetría.
Dibuje la gráfica de la parábola F(X) = -2X2 + 10X - 8, el etiquetado de cualquier intercepta y el vértice y que muestra el eje de simetría.
A continuación se presentan las respuestas a las preguntas de la práctica:
Dibuje la gráfica de la parábola F(X) = 4X2, marcar ninguno intercepta y el vértice y que muestra el eje de simetría.
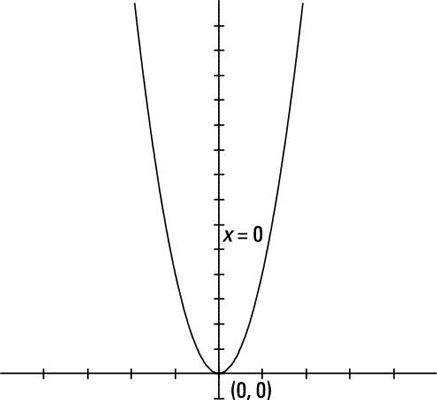
La única intersección está en (0, 0). La parábola se abre hacia arriba, porque 4 es positivo. El vértice está en (0, 0), y la ecuación del eje de simetría es X = 0 (que es el y-eje).
Dibuje la gráfica de la parábola
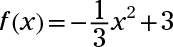
marcar ninguno intercepta y el vértice y que muestra el eje de simetría.
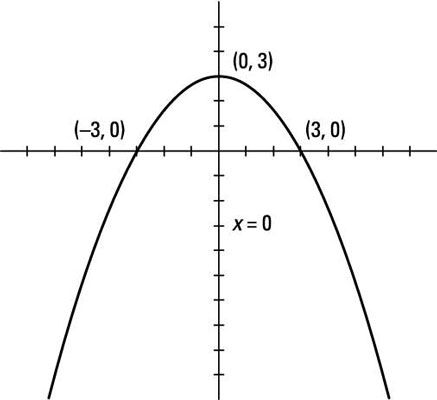
Las intersecciones están en (0, 3), (3, 0), y (-3, 0). La parábola se abre hacia abajo, debido a que el coeficiente de X2 es negativo. El vértice está en (0, 3), el y-interceptar, y la ecuación del eje de simetría es X = 0.
Dibuje la gráfica de la parábola F(X) = 3X2 - 6X - 9, marcar ninguno intercepta y el vértice y que muestra el eje de simetría.
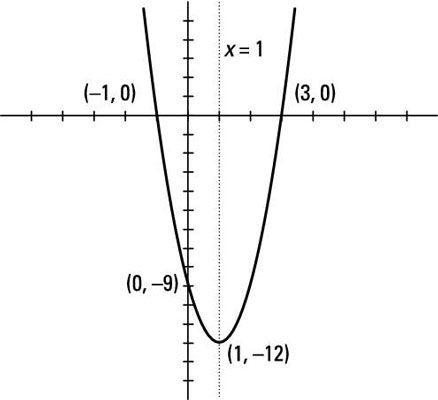
Las intersecciones están en (0, -9), (3, 0) y (-1, 0). La parábola se abre hacia arriba, porque 3 es positivo. El vértice está en (1, -12), y la ecuación del eje de simetría es X = 1.
Dibuje la gráfica de la parábola F(X) = -2X2 + 10X - 8, el etiquetado de cualquier intercepta y el vértice y que muestra el eje de simetría.
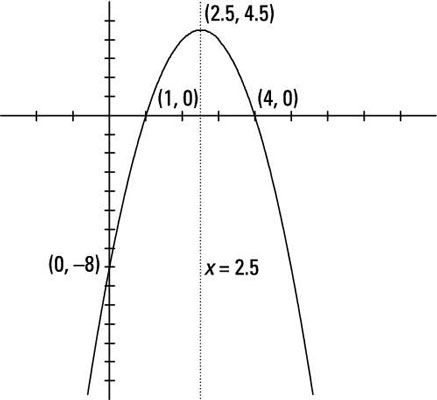
Las intersecciones están en (0, -8), (4, 0) y (1, 0). La parábola se abre a la baja debido a -2 es negativo. El vértice está en (2.5, 4.5), y la ecuación del eje de simetría es X = 2,5.
Sobre el autor
 ¿Cómo encontrar las líneas tangentes de una parábola que pasan por un punto determinado
¿Cómo encontrar las líneas tangentes de una parábola que pasan por un punto determinado ¿Alguna vez quiso determinar la ubicación de una línea a través de un punto dado que es tangente a una curva dada? Por supuesto que tienes! He aquí cómo lo haces.Determinar los puntos de tangencia de las líneas por el punto (1, -1) que son…
 Cómo representar gráficamente una parábola horizontal
Cómo representar gráficamente una parábola horizontal Una parábola horizontal cuenta con sus propias ecuaciones para encontrar su partes- estos son sólo un poco diferente en comparación con una parábola vertical. La distancia al foco y la directriz desde el vértice en este caso es horizontal,…
 Cómo graficar una función coseno
Cómo graficar una función coseno El gráfico de matriz de cosenos se ve muy similar a la gráfica de la función de los padres de seno, pero tiene su propia personalidad chispeante (como mellizos). Gráficos coseno seguir el mismo patrón básico y tienen la misma forma básica…
 Cómo graficar una función racional cuando el numerador tiene el grado más alto
Cómo graficar una función racional cuando el numerador tiene el grado más alto Funciones racionales donde el numerador tiene el mayor grado en realidad no tienen asíntotas horizontales. En cambio, tienen asíntotas oblicuas que se encuentra utilizando la división larga.Por ejemplo, el gráfico h (X):Dibuje la asíntota…
 Cómo graficar una función racional con numerador tiene el grado más alto
Cómo graficar una función racional con numerador tiene el grado más alto Después de calcular todas las asíntotas y la X- y y-intercepciones para una función racional, que tienen toda la información que necesita para empezar a graficar la función. Funciones racionales donde el numerador tiene el mayor grado en…
 Cómo representar gráficamente una parábola vertical,
Cómo representar gráficamente una parábola vertical, Con el fin de representar gráficamente una parábola correctamente, es importante tener en cuenta si es una horizontal o una parábola vertical. Esto es porque mientras que las variables y constantes en las ecuaciones para las dos curvas tienen el…
 Cómo graficar funciones parentales
Cómo graficar funciones parentales En matemáticas, se ve ciertos gráficos una y otra vez. Por esa razón, estas, funciones comunes originales se llaman gráficos de los padres, e incluyen gráficas de funciones cuadráticas, raíces cuadradas, valores absolutos, cúbicas y raíces…
 Cómo graficar polinomios
Cómo graficar polinomios Aunque puede parecer desalentador, graficar polinomios es un proceso bastante sencillo. Una vez que haya encontrado los ceros de un polinomio, puede seguir unos sencillos pasos para representarla gráficamente.Por ejemplo, si ha encontrado los ceros…
 Cómo identificar el mínimo y máximo en parábolas verticales
Cómo identificar el mínimo y máximo en parábolas verticales Parábolas verticales dan una pieza importante de información: Cuando la parábola se abre hacia arriba, el vértice es el punto más bajo en el gráfico - llamado el mínimo, o min. Cuando la parábola se abre hacia abajo, el vértice es el punto…
 Cómo determinar la medida de un ángulo cuyo vértice está en un círculo
Cómo determinar la medida de un ángulo cuyo vértice está en un círculo De los tres lugares vértice de un ángulo puede estar en relación con un círculo (dentro, sobre o fuera del círculo), los dos tipos de ángulos que tienen su vértice en un círculo - inscrito ángulos y ángulos tangente-acordes - son los que…
 Truco Ley para cuadráticas: cómo encontrar rápidamente la ubicación del vértice de una parábola
Truco Ley para cuadráticas: cómo encontrar rápidamente la ubicación del vértice de una parábola Para ahorrar tiempo al graficar una función cuadrática en la prueba ACT de matemáticas, puede encontrar rápidamente la ubicación del vértice de la parábola en relación con el y-eje. Sólo tienes que utilizar el siguiente truco sencillo…
 Truco Ley para cuadráticas: cómo encontrar rápidamente la dirección de una parábola
Truco Ley para cuadráticas: cómo encontrar rápidamente la dirección de una parábola Para ahorrar tiempo al graficar una función cuadrática en la prueba ACT de matemáticas, puede determinar rápidamente la dirección de la parábola usando un simple truco basado en el coeficiente la.Este truco se relaciona con el signo de la…