Cómo graficar las secciones cónicas en forma polar basado en la excentricidad
Al graficar las secciones cónicas en el plano polar, utiliza ecuaciones que dependen de un valor especial conocido como excentricidad, que describe la forma general de una sección cónica. El valor de la excentricidad de una cónica puede decirle qué tipo de sección cónica describe la ecuación, así como la forma de grasa o flaca que es.
Al graficar ecuaciones en coordenadas polares, es posible que tenga problemas para contar qué sección cónica debe estar Graficando basan únicamente en la ecuación (a diferencia de la representación gráfica en coordenadas cartesianas, donde cada sección cónica tiene su propia ecuación única). Por lo tanto, puede utilizar la excentricidad de una sección cónica para saber exactamente qué tipo de curva que usted debe gráfica.
Aquí están las dos ecuaciones que permiten poner las secciones cónicas en forma de coordenadas polares, donde (r, theta) es la coordenada de un punto de la curva en forma polar. Recordemos que r es el radio, y theta es el ángulo en posición estándar en el plano de coordenadas polares.
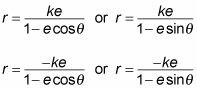
Al graficar las secciones cónicas en forma polar, puede conectar varios valores de theta para obtener la gráfica de la curva. En cada ecuación anterior, k es un valor constante, theta toma el lugar de tiempo, y e es la excentricidad. La variable e determina la sección cónica:
Si e = 0, la sección cónica es un círculo.
Si 0 lt; e lt; 1, la sección cónica es una elipse.
Si e = 1, la sección cónica es una parábola.
Si e > 1, la sección cónica es una hipérbola.
Por ejemplo, digamos que usted desea graficar esta ecuación:
La primera cosa que hay que hacer es hacer el denominador empezar 1. Este denominador comienza con 4, por lo que tiene que factor que 4 para saber lo que k ¡es!
Factoring el 4 del denominador que [da
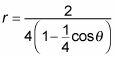
A fin de mantener la ecuación cerca de la forma estándar para las cónicas polares, multiplicar el numerador y el denominador por 1/4. Este paso le da
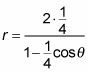
Por lo tanto, la constante k es media y la excentricidad, e, es 4.1, que le dice que usted tiene una elipse, porque e está entre 0 y 1.
Para graficar la función polar de esta elipse, se puede conectar en los valores de theta y resolver r. Luego trazar las coordenadas de (r, theta) en el plano de coordenadas polares para obtener la gráfica. Para la gráfica de la ecuación ejemplo,
usted puede conectar
y encontrar r en cada caso:
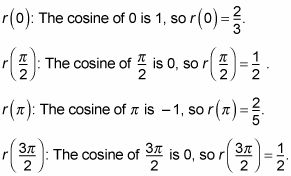
Estos cuatro puntos son suficientes para darle un esbozo de la gráfica.
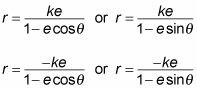
Usted puede ver la gráfica de la elipse ejemplo en esta figura.
-
Convertir desde rectangulares a coordenadas polares en la TI-83 Plus -
Evaluar expresiones polares en la TI-83 Plus -
Encuentra derivados de ecuaciones polares con la TI-83 Plus -
Cómo ingresar ecuaciones polares en la TI-83 Plus -
Cómo graficar varias ecuaciones polares en la TI-83 Plus -
Cómo ingresar ecuaciones polares en la TI-84 Plus
Cómo graficar ecuaciones polares en su TI-84 Plus Después de configurar la ventana y entró en la ecuación polar, graficar las ecuaciones en la TI-84 Plus es fácil. Antes de pulsar [GRÁFICO], asegúrese de que usted mira la dirección que se crea el gráfico. Si tu # 952 pasos es lo…
Matemáticas normas fundamentales comunes: propiedades geométricas como ecuaciones Los estudiantes utilizan lo que saben acerca de las operaciones de álgebra para demostrar (o probar) ciertos aspectos o características de formas geométricas de las normas fundamentales comunes. Por ejemplo, si usted sabe que los tres ángulos…
Completando el cuadrado para las secciones cónicas Cuando la ecuación de una sección cónica no está escrito en su forma estándar, completando el cuadrado es la única manera de convertir la ecuación a su forma estándar. Los pasos del proceso son los siguientes:Añadir / restar cualquier…
Las secciones cónicas en pre-cálculo Las secciones cónicas puede ser descrito o ilustrado con exactamente lo que su nombre indica: conos. Imagina un cono anaranjado en la calle, que dirigir en la dirección correcta. Entonces imaginar algún ingeniero de caminos inteligente colocar un…
Cómo cambiar entre coordenadas polares y cartesianas Puede utilizar ambas coordenadas polares y cartesianas (x, y) coordenadas (también conocidas como coordenadas rectangulares) en cualquier momento para describir la misma ubicación en el plano de coordenadas. A veces, usted tendrá un tiempo más…
Cómo graficar las secciones cónicas en forma paramétrica A veces, su profesor de pre-cálculo puede pedirle que gráfico de una cónica en forma paramétrica. Forma paramétrica es una forma elegante de decir una forma en la que usted puede hacer frente a las cónicas que no se expresan fácilmente como…
2 maneras de graficar un círculo Círculos son fáciles de trabajar en pre-cálculo. Un círculo tiene un centro, un radio, y un montón de puntos, pero sigue pasos ligeramente diferentes, dependiendo de si está mostrando el gráfico de un círculo centrado en el origen o desde el…
Cómo graficar coordenadas polares con valores negativos A veces, su profesor de geometría puede condimentar un poco las cosas con complicados coordenadas polares - señala con ángulos y / o radios negativos. La siguiente lista muestra cómo trazar en tres situaciones - cuando el ángulo es negativo,…
Cómo identificar las cuatro secciones cónicas en forma de ecuación Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…
Cómo identificar las cuatro secciones cónicas en forma de gráfico Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…
Cómo trazar coordenadas polares Coordenadas polares son una adición muy útil a su caja de herramientas matemáticas, ya que permiten a resolver los problemas que serían muy feo si tuviera que depender de norma X- y y-coordenadas. Con el fin de comprender plenamente cómo trazar…
¿Cómo resolver sistemas no lineales En un sistema no lineal, al menos una ecuación tiene una gráfica que no es una línea recta - es decir, al menos una de las ecuaciones tiene que ser no lineal. Su instructor de pre-cálculo le dirá que siempre se puede escribir una ecuación…