Cómo graficar las secciones cónicas en forma paramétrica

A veces, su profesor de pre-cálculo puede pedirle que gráfico de una cónica en forma paramétrica. Forma paramétrica es una forma elegante de decir una forma en la que usted puede hacer frente a las cónicas que no se expresan fácilmente como la gráfica de una función y = F(X). Las ecuaciones paramétricas se utilizan generalmente para describir el movimiento o la velocidad de un objeto con respecto al tiempo. Usando las ecuaciones paramétricas le permite evaluar tanto X y y como variables dependientes, en lugar de X ser independiente y y depende de X.

Forma paramétrica define tanto la X- y el y-variables de las secciones cónicas en términos de una tercera variable, arbitraria, llamada parámetro, que por lo general está representado por t. Usted puede encontrar los valores para ambos X y y enchufando valores para t en las ecuaciones paramétricas. Como los valores de t cambio, también lo hacen los valores para X y y, Lo que significa que y ya no es dependiente de X pero es dependiente de t.

¿Por qué cambiar a esta forma? Consideremos, por ejemplo, un objeto que se mueve en un plano durante un intervalo de tiempo específico. Si un problema le pide que describa la trayectoria del objeto y su ubicación en cualquier momento determinado, se necesitan tres variables:

• Hora t, que por lo general es el parámetro

• Las coordenadas (x, y) Del objeto en el momento t

los X_t ecuación da el movimiento horizontal de un objeto como t cambios- el y_t ecuación da el movimiento vertical de un objeto con el tiempo.

Por ejemplo, un conjunto de ecuaciones define tanto X y y para el mismo parámetro - t - y define el parámetro en un intervalo establecido:

Hora t existe sólo entre 1 y 5 segundos para que este problema.

Si se le pregunta a graficar esta ecuación, puede hacerlo en una de dos maneras. El primer método es el enchufe y chug: Establecer un gráfico y recoger t valores del intervalo dado con el fin de averiguar lo que X y y debe ser, y luego graficar estos puntos como normal. La siguiente tabla muestra los resultados de este proceso. Nota: t = 1 se incluye en la tabla, aunque el parámetro no está definido allí. ¡Tienes que ver lo que hubiera sido, porque graficar el punto donde t = 1 con un círculo abierto para mostrar lo que ocurre con la función arbitrariamente cerca de 1. Asegúrese de hacer de ese momento un círculo abierto en el gráfico.

La otra manera de representar gráficamente una curva paramétrica es resolver una ecuación para el parámetro y luego sustituir esa ecuación en la otra ecuación. Usted debe escoger la ecuación más sencilla de resolver y empezar por ahí.

Siguiendo con el mismo ejemplo, resolver la ecuación lineal X = 2t - 1 de t:

1. Sustituya los puntos finales de la t en el intervalo X función de saber dónde está el gráfico de arranques y paradas.

   Esto se hace en la tabla. Cuando t = 1, X = 1, y cuando t = 5, X = 9.

2. Resolver la ecuación más simple.

   Para la ecuación elegida, se obtiene

3. Conecte la ecuación resuelto en la otra ecuación.

   Para este paso, se obtiene

   

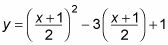
4. Simplifique esta ecuación si es necesario.

   Ahora tiene

   

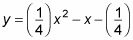
   Debido a este paso le da una ecuación en términos de X y y, puede graficar los puntos en el plano de coordenadas. El único problema es que no dibuje toda la gráfica, ya que hay que mirar en un intervalo específico de t.

   
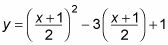   Representación gráfica de una curva paramétrica.

Esta figura muestra la curva paramétrica de este ejemplo (para ambos métodos). Se termina con una parábola, pero usted también puede escribir ecuaciones paramétricas para elipses, círculos y hipérbolas.